什么是张量？

https://www.bilibili.com/video/BV1tr4y117Ja/

常数 a 是 0 阶张量向量 \(\vec{a}\) 是 1 阶张量用 \(\widetilde{A}\) 表示 2 阶以上的张量

张量是一种不依赖于坐标系来反应物质的物理量。

向量 \(\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}\) 不会因为坐标系的变化而变化。

那么一个二阶矩阵是张量吗？

\[ \left [ \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} \right ] \]

二阶的一个矩阵不是一个张量。

\(\widetilde{A}=A_{ij}\vec{e_{i}}\vec{e_{j}}\) ，其中 \(A_{ij}\) 是数，称之为张量的分量。而后面的 \(\vec{e_{i}}\vec{e_{j}}\) 表示基矢量并矢。

比如 \(\vec{a}=5\vec{i}+6\vec{i}+7\vec{z}\) 其中的 \(\vec{i}\) ， \(\vec{j}\) ， \(\vec{k}\) 表示基矢量。这三个会张满整个空间。

什么是并矢呢？

把两个张量并排的写在一起。 \(\tilde{A}\tilde{B}\) 这就是并矢。如是 \(\tilde{A}\) 是 m 阶的张量， \(\tilde{B}\) 是 n 阶的张量。则两个的并矢是 \(m+n\) 阶的张量。用三维坐标系来表示的话就是 \(\vec{x}\) ， \(\vec{y}\) 合起来表示成一个平面，也就是升阶了。

矩阵可以看成是一个 0 阶的张量。因为矩阵没有基矢量的定矢。现在关注一下 \(A_{ij}\) ，这个数可以有很多种的表示的形式，它是可以用矩阵来表示的。张量分量是一个数，矩阵形式的张量分量也是一个数。可以这么写：

\[ \left [ \begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{matrix} \right ] \]

有时候只写一个矩阵的话，是省略了基矢量并矢的。一个矩阵的本质是一个函数，比如 \(i=1,j=2\) 的话就是表示 \(A_{12}\) 。这里面的两个亚标都是 i 和 j ，张量表示是一个遍历的全部过程。两次求和。

什么是 \(\delta_{ij}\) ，这个函数是什么？

\[\delta_{ij}=\begin{cases} 1, & i=j \\ 0, & i\neq j \end{cases} \]

什么是 \(\epsilon_{ijk}\) ，这个函数又是什么？

\[ \epsilon_{ijk}=\begin{cases} 1, & odd\\ 0, & equal\\ -1, & even \end{cases} \]

因为是数，所以可以移动位置。张量分量的矩阵形式就是用矩阵来表示，但是如果要用张量形式的话，就不能用矩阵来表示。

张量的简写： \(\tilde{P}=P_{ij}\vec{e_{i}}\vec{e_{j}}=\{P_{ij}\}=P_{ij}\) 这是在直角坐标系下的一种简写形式。所以 \(\delta_{ij}\) 有时候是一个数，有时候是一个张量，是不一样的。

几个特殊的张量：delta 函数，epsilon 函数，爱因斯坦求和约定，nabla 算子，Detla 算子。

(1) 第一个就是 \(\delta_{ij}\) 张量。

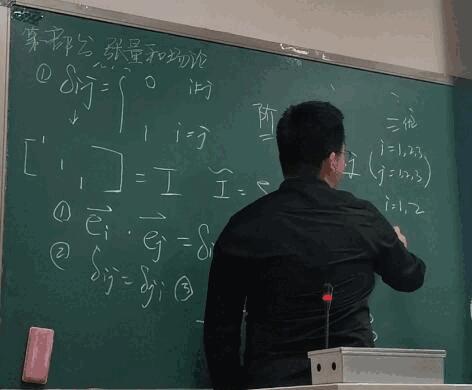
(2) 第二个是 \(\epsilon_{ijk}\) 张量。为什么那么设计呢，是因为要符和右手定则，函数的构造都是为了方便计算的。叉乘或叫乘积。

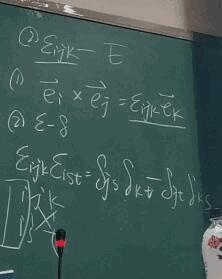
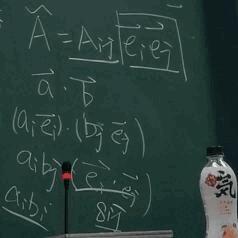
矢量，张量的运算，本质上是基矢量并矢的计算，与张量分量无关。下标这里称之为亚标。亚标数和维数是两个不同的概念。比如下面二阶的张量在三维的坐标下的运算。张量的计算也是求和。

\(a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\)

\(\vec{a} \times \vec{b} = \epsilon_{ijk}a_{i}b_{j}\vec{e_{k}}\) 第一部分是数，也能表征右手定则，表示正负；第二部分也是数，以模的形式表示在前面；最后一部分表示方向。这个就是爱因斯坦求和约定，很漂亮的形式。

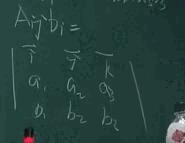
矩阵的形式不如张量的形式，张量的形式能表示出右手定则，更直观一点。

机器学习当中的张量

https://blog.csdn.net/wohu1104/article/details/105603829

机器学习当中的张量就是高维数组这种数据结构做的，和张量分析当中的张量有所不同。高阶的矩阵表示高维当中的一种线性变换。那做了多次的线性变换就是多重线性变换了，也就是张量描述的东西。

说万物可矩阵，万物可张量，都是对的。这是用到了抽象的符号。抽象的符号组织的很好了之后，可以方便人们发现更多的规律，就是这们回事。矩阵是变换也是一个数，是 0 阶张量，但也是张量，这样看 tensorflow 当中称为 tensor 也没有什么奇怪的了。

可就是对数据的多次变换就是 tensor flow 了。数学专业的定义和机器学习的定义也不完全一样。机器学习对数学概念的使用比较随意，不用很在意这些名词。要在意的是一些函数的由来。