矩阵的导数

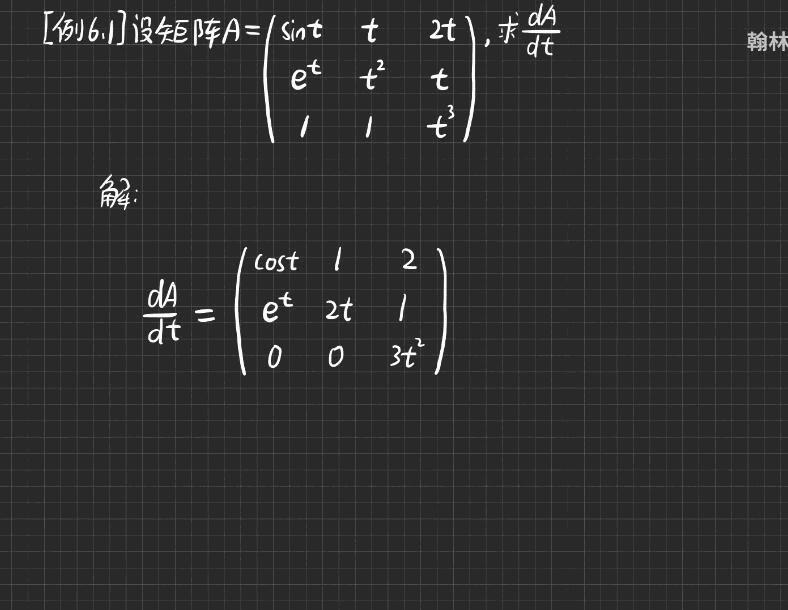
之前的目的是看明白反向传播算法的推导过程。现在怎么觉得这个不像呢?
矩阵的幂级数

上面的 2 当中的 \(\rho(A)\) 是谱半径,也就是所有的特征值当中最大的那个。3 当中的 \(\rho\) 是曲率半径。
毛主席当年也是叛逆少年。但是他的叛逆是一种正确的方式,而不是盲目发泄或全盘否定。性格的影响是极为重要的。犯浑的人往往是头脑不清晰。有一个清晰的头脑之后,自然而然会走正确的道路。


重点:矩阵函数

什么是矩阵函数?这里看不太明白。什么是最小多项式?之前学过。
我现在工作生活的与躺平无异。你躺你的孩也学你躺平。



为什么题目让求 \(e^{At}\) 因为它好算,也可以是 \(\sin At\) 或者 \(\cos At\) 。


计算量大。高级的要求是熟练度。因为熟练度高意味着一件事一个人努力了,去尝试做到极限了。熟练度真的是对一个人的最高要求了。算的准之后才是快。做到了又准又快,那么一个人也就成为了这个领域的牛人了。
技能都是一项一项学的。把关键的练到最快。比如五笔能做到击键九次,那就是一个普通人的极限了。看不懂公式搞人工智能就是空中楼阁。看不懂时候不要想着快,快是懂了之后才练的。
矩阵在微分方程组中的应用

我对这个世界的复杂性没有足够的认识。想让别人认可,要拿出来大家统一标准的评价体系下的成果。这才能让人信服。在多数情况下公共评价体系是相对科学与公平的。一个人总是觉得自己与众不同是没有意义的。在大的领域有出类拔萃的成果才是人才。


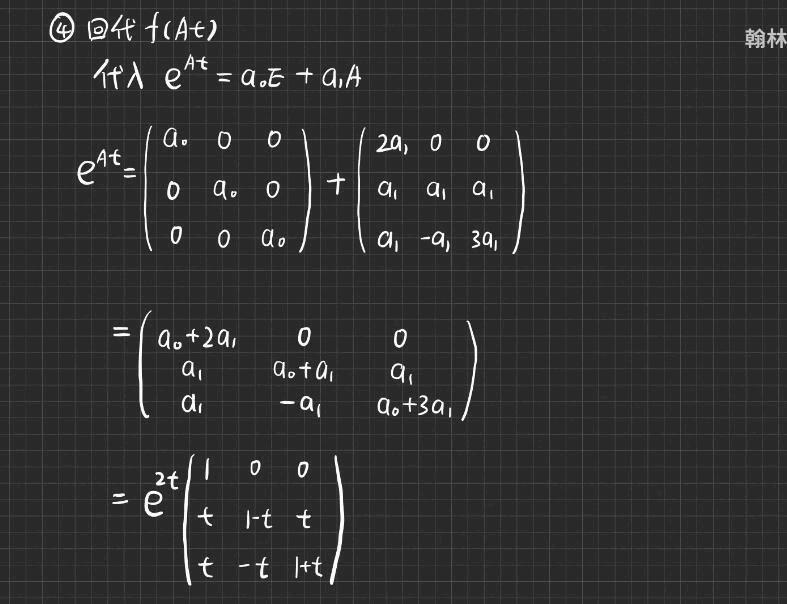

上面的的 \(\tau\) 是变量,手写的 \(\tau\) 看着很像是 “2” 。做研究写论文,这些公式要学会,是必不可少的。
矩阵函数的性质
由 \(A\) 求 \(e^{At}\) 很麻烦,但是由 \(e^{At}\) 求 \(A\) 比较简单。

数学符号的背后是逻辑。上面的公式是可以证明的, up 主没有证明,这个证明我反正是想不到的。
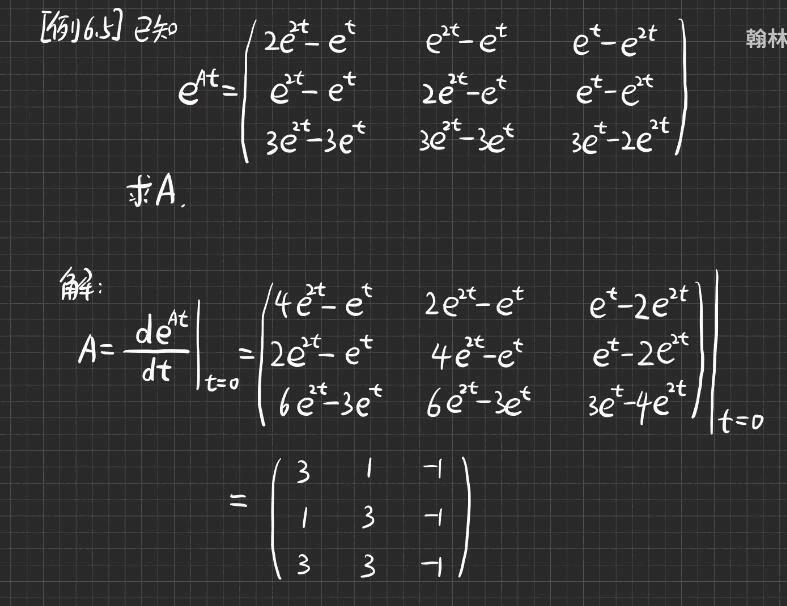
此处就是矩阵函数求导的方法。
后续还有张量分析这门课。张量的本质就是“多重线性映射”,入门张量分析,再反过头看之前一个博客中讲机器学习的本质。还是不懂,继续学。
