矩阵的三角分解

单位下三角矩阵。普通上三角矩阵。矩阵的分解有什么用呢?L 是左, R 是右。

上面黄色的部分是直接抄下来的。 \(a_{21}\) 是第二行乘以第一列这么算的。

暂时感觉 Crout 分解法和 Cholesky 分解法没有什么用处。先不看了,以后有兴趣了再看一下。
矩阵的 QR 分解

计算题都是套路,或者说是算法。Q 是酉矩阵。用施密特正交化法。我感觉矩阵分析就是线性代数多了一些内容。
数学专业和非数学专业学习数学的区别,学数学专业的课能增加自信。但是想在考研数学中取得好成绩,熟练度是更为重要的。


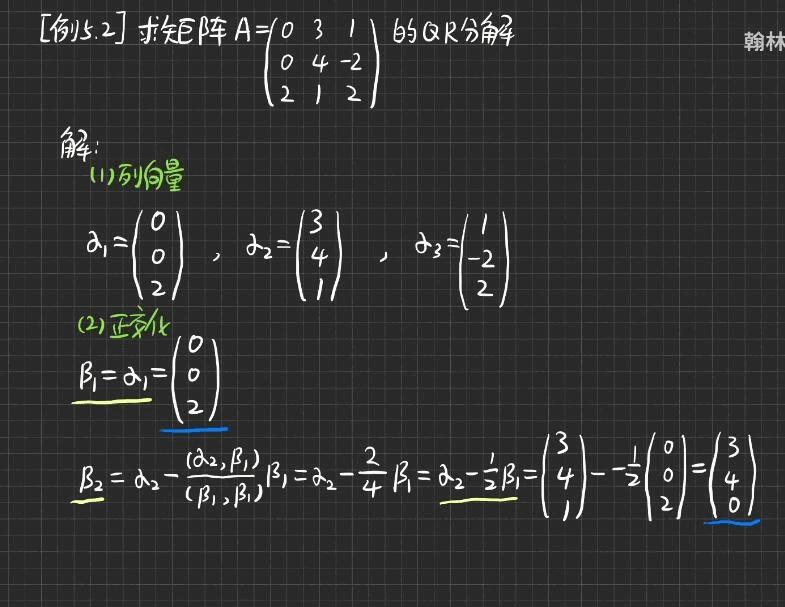


https://www.zhihu.com/question/322658703 ,数学系和考研数学的差距。看完之后知道自己是底子是非常差的。但不要恢心,我还可以抢救一下。
矩阵的满秩分解

我们学的这些东西是很多数学家一辈子的研究成果。看不懂学不会是正常的。多学几篇就明白了。就懂了。
什么是满秩矩阵?
若矩阵秩等于列数,称为列满秩。既是行满秩又是列满秩则为 n 阶矩阵即 n 阶方阵。行满秩矩阵就是行向量线性无关,列满秩矩阵就是列向量线性无关;
设 A 是 n 阶矩阵, 若 r(A) = n , 则称 A 为满秩矩阵。 满秩矩阵是一个很重要的概念,它是判断一个矩阵是否可逆的充分必要条件。


先化成阶梯型。再化成行最简,什么是行最简?
在阶梯形矩阵中,若非零行的第一个非零元素全是 1,且非零行的第一个元素 1 所在列的其余元素全为零,就称该矩阵为行最简形矩阵。
矩阵提取系数的方法:
格局要打开,否则经常会意难平。
一旦一个问题可以用矩阵来描述,那么,这个问题用矩阵的法则来求解求可以了。而你还在纠结矩阵各种规律是怎么推导的时候,物理学家已经开始熟练的使用他们来描述理论了。同时 AI 的科学家们也没有去探讨最为深刻的数学规律。做人,做学问,做工程,某一时刻总有最该注意的问题,总有最有价值的问题,总有最重要的问题。
穷人的觉悟就是努力成为一个富人;底层的觉悟就是努力学习提升认知的水平。穷则变,变则通。躺平有罪,苟活无益。多要求自己,就算你的父母子女优秀也不如你自己优秀更令自己愉快,人的本质都是追求个人的奋斗。别人的成功与你无太大关系,就算是你绐予下一代足够的关心令之成长也无法弥补自己这一代的平庸的痛惜。人生的路,退无可退,唯有向前。
让实力配上你天生的阿斯伯格。走向成熟,要是再不成熟的话,一辈子都要过去了。另外成熟不是没有梦想,而是用现实的方法追求梦想。

我怀疑上面的 P 写错了, \(\frac13\) 那块化简的好像有问题,以后再看。这是计算部分。没有写错,这是矩阵的标量乘法。
上面的内容没有问题。你要分清楚矩阵和行列式。行列式记作 \(\overline{A}\) 或 \(\det(A)\) ,而 \(A\) 代表矩阵:矩阵的标量乘法遵循分配律和结合律,是所有元素都乘以标量的乘数。而行列式的的标量乘法则不同,是这个公式:
\(|kA|=k^{n}|A|\)
上面的行化简完后 r=2 ,则:
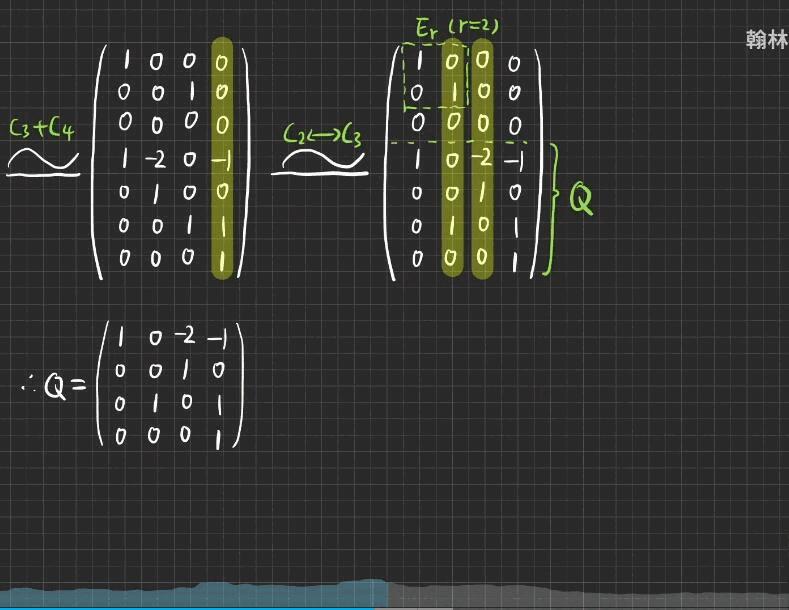

满秩分解有什么用处?https://blog.csdn.net/guoziqing506/article/details/80540323 在机器学习里面很有用。所以矩阵分析是很重要的。
奇异值分解,十年没有考。但是这个在科研上非常的重要。
https://www.cnblogs.com/marsggbo/p/10155801.html 这篇文章讲了一下奇异值分解,要想理解清楚,肯定要自己做题多演算的。这些东西肯定比较复杂,但是一定要搞清楚。人工智能用到的数学主要是各种矩阵,起码我现在看到的是这样的。
发现一个博客,他在 2017 年就开始了我最感兴趣的方向。
https://www.cnblogs.com/marsggbo ,他的微信公众号是 AutoML 机器学习。
别人的知识结构和你的不一样,可以参考,但是要自己重新走一遍。
