第三章是矩阵的标准形
哈密顿-卡莱定理
数学的本质就是逻辑与设定,如果你觉得反常识那是对设定理解的不深刻。如果推导的速度慢,那是逻辑能力差。

韩国考上 SKY 三所好学校的概率和中国考上 985 的概率是差不多的。在中国考上顶尖 985 或者靠竞赛上一个 985 或者是北大数学系物理系,那么科研之路就有了可能,最后读个 PHD 上岸。
上面的定理非常重要。det 是 determinant 的意思,计算出行列式的结果。这个英文单词的意思是决定性因素,决定条件,也有行列式,方阵的意思。
https://www.ldoceonline.com/dictionary/determinant 从网上的朗道英文词典中能够查到,这个词的真实意思,这样就理解这个词的英文内核了。
什么是特征多项式?
特征多项式是指将一个方阵的特征值 \(\lambda\) 带入到多项式中所得到的多项式。在线性代数中,特征多项式是一个非常重要的概念。
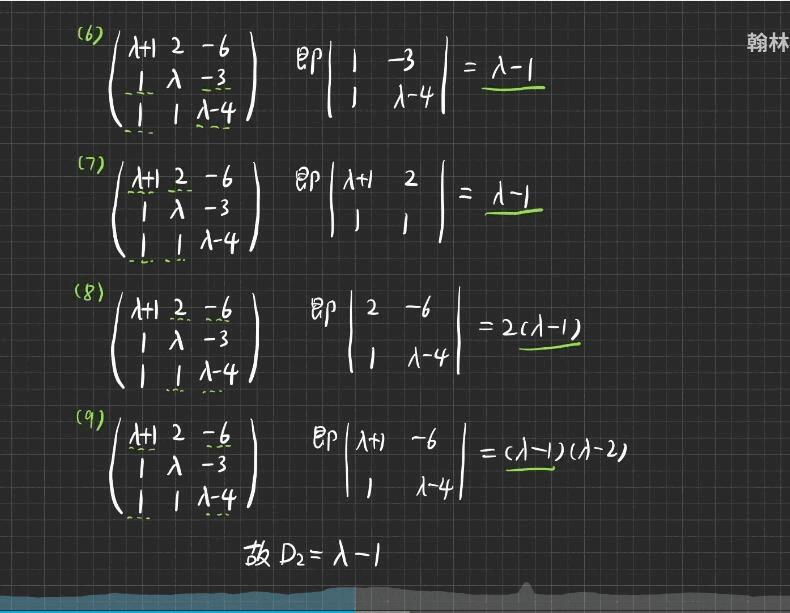
对于一个 \(n \times n\) 的方阵 \(A\),其特征多项式 \(P(\lambda)\) 定义为:
\(P(\lambda) = det(A - \lambda I)\)
其中,det(·) 表示矩阵的行列式运算,I 表示单位矩阵。
特征多项式 \(P(\lambda)\) 是一个关于 \(\lambda\) 的 \(n\) 次多项式。它的每一项的系数都与原方阵 \(A\) 有关。展开特征多项式后,可以得到类似下面的形式:
\(P(\lambda) = (-1)^n \lambda ^n + c_{n-1} \lambda^{n-1} + c_{n-2} \lambda^{n-2} + … + c_1 \lambda + c_0\)
其中 \(c_{n-1}\) 、 \(c_{n-2}\) 、…、 \(c_1\) 、 \(c_0\) 是与矩阵 \(A\) 相关的常数系数。
特征多项式的根(即使 \(P(\lambda) = 0\) 成立的 \(\lambda\) 值)就是原方阵 \(A\) 的特征值。
特征多项式在很多应用中起着重要的作用,例如特征多项式可以用来计算矩阵的特征值和特征向量。通过求解特征多项式的根,我们可以找到方阵的特征值,进而求解对应的特征向量。特征多项式还可以在矩阵的对角化、奇异值分解等问题中发挥关键作用。
总之,特征多项式是一个与方阵特征值和特征向量紧密相关的多项式,它为我们理解和应用矩阵的特征值提供了基础。
wiki 上有卡莱-哈密顿定理的证明:
这么重要的一个定理,想自己会证明要思考的问题比较多。可以学,可以模仿。经常要跳出问题本身。这才是解决数学问题比较重要的地方。
每门学科都是不容易的,因为都涉及到几个核心公式。


上面这道题的求解公式非常的精彩。中国的是记公式,而不是求解公式。
考点二:最小多项式

最不多项式,重中之重。对矩阵求导有很重要的作用。上面写的是 \((n_{i} \le k_{i})\) ,

行列式的按行展开是: \((-1)^{i+j}M_{ij}\) ,其中的 \(M_{ij}\) 是原行列式的代数余子式。记一个就行了,如果想按列展开,做一下转置就行了。行列式做完转置的值与原值相等。
考点三:约当标准型(Jordan 标准型)

这个是法国数学家,所以叫约当(若当)标准型。上图不清楚的地方是 \(D_{k}(\lambda)\) 。
 约当块,约当标准型。
约当块,约当标准型。
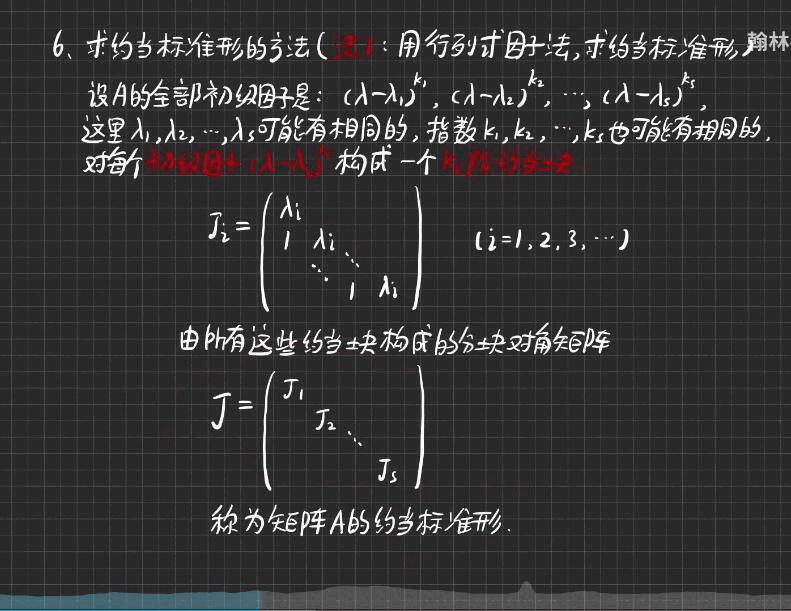
就算是最聪明的人也不可能将所有的这些东西学会:
参考下面这个帖子,数学专业和非专业的学生差距有多大:
https://www.zhihu.com/question/31196397
数学是什么,数学是符号和逻辑。所以数学的概念是无穷无尽的。只要是世上有的东西,都可以归为研究的对象,甚至这个世界上没有的东西,也可以用抽像的方法去研究。数学的目的还是为了探索和创造,这种东西。若想成功不能够没有边际的学习。人的一生就是有寿命长短的,是有边际的。所以在了解了一定的广度之后,一定要选择一个方向回归。若说之前可以有强人可以对大部分的分支都做出贡献,那是还没有经过 20 和 21 世纪的科技大爆炸。
希尔伯特,冯·诺依曼,庞加莱。不是大神越来越少了。而是分支太多,没有时间理解那么多的背景问题。
我对自己的定位是什么?我是一个工程师,要学会别人的理论用于解决问题。不用对理论的认识十分的深刻,但是要把有用的东西用对地方。能做到这一点也不能说是一个失败的人,也许不如自己对自己之前的要求那么高。学一点比不学一点强。任何的爱好都是有价值的,有和没有是不同的。保障生活的前提下,有追求是有好处的。希望你幸运,能从中得到足够满足自己的收获。



出现的次数是含义就是,如果有两个 \((\lambda -1)^{2}\) 的话,对角线上再多写一个“三个 1”的块就行了。\(\lambda\) 剪的那个数就是对角线的数。约定在对角线外的值一般放在下面。
最关键的,一定要充分理解的是矩阵求导部分的基础知识,这块对 AI 的重要性太大了。
如果有 \(d_{4}=(\lambda-2)^{2}(\lambda-1)\) 的话,要拆成:\((\lambda-2)^{2}\) 和 \((\lambda-1)\),一定要拆成两个,否则结果是不对的。

三个块可以任意组合。理论数学家为工程师提供工具。计算机的重大理论突破在数学上没有任何突破,但是有的问题会不会有呢?会的,比如平铺问题,四色问题。
这个世界是相辅相成的关系。关键是找到有价值的东西,并在真正有价值的地方取得突破。认识到这一点,你就真正的豁然开朗了。
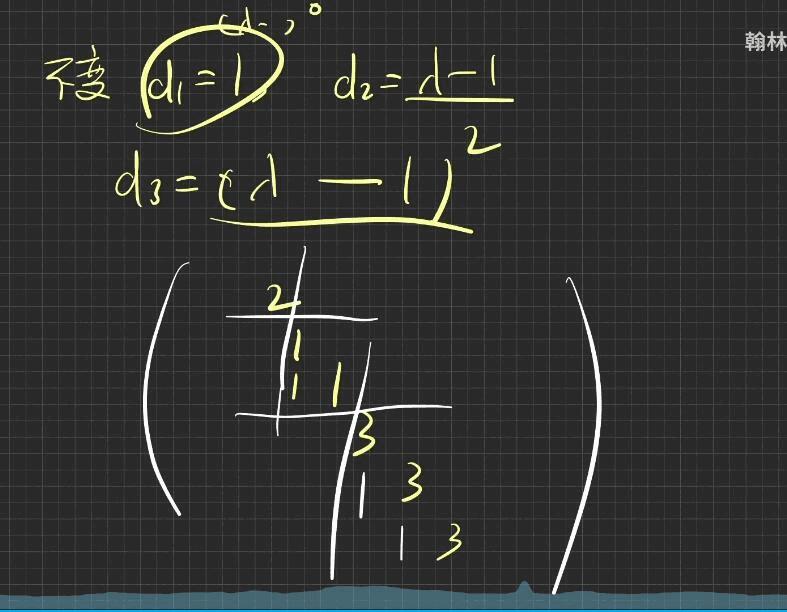
所有的关系都要写出来。
史密斯标准型
你是天才吗?不是的话,不要想着一遍就学会。无他,唯手熟尔。

重点,smith 标准型。
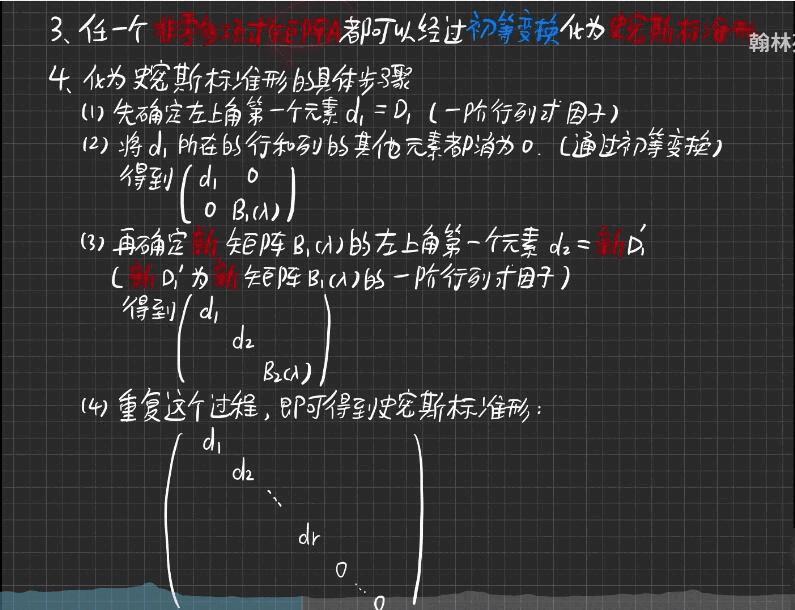


用史密斯标准型方法求解约当标准型



贪多嚼不烂,慢慢理解,有的时候慢下来总结反而是一种更快的方法。
