数学往往只讲理论，不讲应用。这就很让人摸不着头脑。

内积空间

什么是内积空间（也叫准希尔伯特空间）？什么是酉空间？wiki 上的解释也太抽象了。什么是完备化？

简单来说内积是对点积增加复数域的推广，内积空间就是酉空间。共轭转置是复数的概念：

共轭转置是一个操作，用于将复数或矩阵中的每个元素取共轭，并进行转置。对于一个复数 a + bi，它的共轭转置为 a - bi。对于一个矩阵而言，共轭转置操作将每个元素取共轭，并将矩阵转置。

以矩阵为例，设 A 是一个 m×n 复矩阵，其共轭转置记作 A*（读作"A dagger"）。通过共轭转置操作，A* 的第 i 行、第 j 列的元素是 A 的第 j 行、第 i 列元素的共轭。换句话说，如果 A 的第 i 行、第 j 列元素为 a+bi，则 A* 的第 i 行、第 j 列元素为 a-bi。

共轭转置常用于复向量空间和矩阵运算中，例如定义内积、计算共轭梯度法等。它在许多数学和工程应用中发挥重要作用。

内积空间（inner product space）是一种代数结构，它在数学中具有广泛的应用。一个实内积空间是一个实向量空间，配合一个称为“内积”的函数来定义向量之间的乘法。内积类似于向量的点积，但它可以定义于更一般的向量空间上，并且具有更一般的性质。

内积可以看作是两个向量之间的“相似度”或“夹角”。内积空间具有许多重要的性质，包括范德蒙恒等式、柯西-施瓦茨不等式和三角不等式等。内积空间是线性代数研究的重要分支，应用广泛，例如量子力学、信号处理、数值计算、图像处理等领域。

内积空间又称为准希尔伯特空间。希尔博特空间要学习泛函分析（function analysis）。代数相比于几何更加的抽象。

https://www.cnblogs.com/ben-ben/articles/3391781.html

这篇文章讲得真的是特别的好啊，可惜我没有机会再学数学专业了。希尔博特空间的完备性其实就是对无穷级数的研究。这方面的研究让数学上所有函数可以用几何来表示。几何又可以通过矩阵来表示，那么，就像计算机中的函数式语言 lisp 一样。这个世界是对象（静态的），还是函数（动态的）完全取绝于看问题的角度。

这个世界是啥？

动与静与时间，时间到底存在吗？静态和动态本质上是一样的，那其实时间这个概念和以太有点像，可能根本就是不存在的。不是一个根本的东西。

时间可能是一种约束，就像希尔伯特空间要求的无穷维中范数的收敛。在现实生活中，我们不能做的事就是改变过去，但我们可以影响未来。这是一种热力学中熵增类似的概念。有可能对于过去，这个世界是收敛的，而对于未来这个世界是发散的。

泛函分析已经成为现代数学的重要支柱之一。看完了这些东西，理解上面的 B 站中的概念就十分地简单了。线性代数的理解好像也豁然开朗了。

标准正交积

schmidt，英文的单词也要懂。

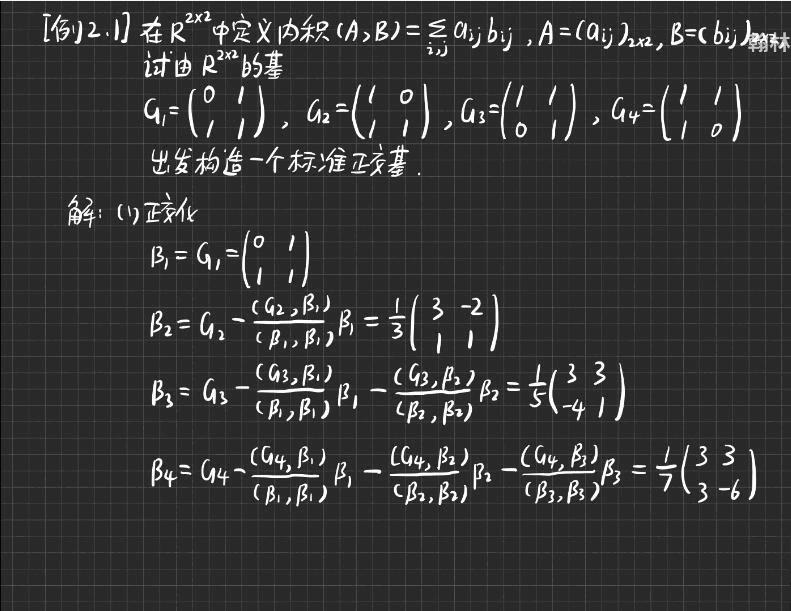
正规矩阵

上图中的 \(A^{H}\) 为 \(A\) 的共轭矩阵。

• 酉矩阵

酉：单一的，统一的。unitary，集权的，单一自治的。拉丁字母 U 来表示。所以中文的这个酉字用的还是很好的。音，义两方面都是“达”的。

在线性代数中，幺正矩阵（又译作幺正矩阵，英语：unitary matrix）指其共轭转置恰为其逆矩阵的复数方阵，数学描述如下：

（数学定义）:

\({\displaystyle U^{*}U=UU^{*}=I_{n}}\)

其中 \(U^{*}\) 是 \(U\) 的共轭转置， \(I_{n}\) 是 \(n\times n\) 单位矩阵。

幺正矩阵是正交矩阵（元素均为实数）在复数的推广。

• 对角矩阵（Diagonal Matrix）

就是只有对角线上有非零元素。

\[ \notag \left [ \begin{matrix} a& 0& 0 \\ 0& b& 0 \\ 0& 0& c \end{matrix} \right ] \]

• 实对称矩阵（Real Symmetric Matrix）

\[ \notag \left [ \begin{matrix} a& b& c \\ b& d& e \\ c& e& f \end{matrix} \right ] \]

是指一个方阵，它满足以下两个条件：

1.矩阵的元素都是实数。

2.矩阵的转置等于它自己，即 \(A = A^T\) 。

即 \(A=A^{T}\) 且在实数域上。

• 反实对称矩阵（Skew-Symmetric Matrix）

英文的原义就是倾斜-称的意思，学数学还要学很多的英文，法文和拉丁文。

是指一个方阵，它满足以下两个条件：

1.矩阵的元素都是实数。

2.矩阵的转置等于它相反数的乘积，即 \(A = -A^T\) 。

\[ \notag \left [ \begin{matrix} 0& a& b \\ -a& 0& c \\ -b& -c& 0 \end{matrix} \right ] \]

• 厄米特矩阵

也称自共轭矩阵，也称自伴随矩阵。名字很多，关键是理解其形式。

厄米特矩阵（Hermitian Matrix）是指一个复数方阵，它满足以下两个条件：

1.矩阵的元素都是复数。

2.矩阵的共轭转置等于它自己的转置的复共轭，即 \(A = A^*\) ，其中 \(A^*\) 表示矩阵 \(A\) 的共轭转置。

换句话说，厄米特矩阵的每个元素关于主对角线对称，并且每个元素与其对应位置的元素的共轭相等。主对角线是从左上角到右下角的一条对角线。

\[ \notag \left [ \begin{matrix} a& b& c \\ b^{*}& d& e \\ c^{*}& e^{*}& f \end{matrix} \right ] \]

其中，a、b、c、d、e、f 都是复数，并且矩阵的共轭转置等于它自己的转置的复共轭 \(A = A^H\) 。

厄米特矩阵具有一些重要的性质和特点：

1.厄米特矩阵的主对角线上的元素都是实数。

2.厄米特矩阵的特征值都是实数，且它的特征向量对应的特征值之间是正交的。

3.厄米特矩阵可以通过酉相似变换对角化。这意味着可以找到一个酉矩阵，将厄米特矩阵相似变换为一个对角矩阵，即将矩阵的非对角线上的元素全部变为零。

\(a_{{i,j}}=\overline {a_{{j,i}}}\) ，其中 \(\overline{(\cdot)}\) 为共轭算子。

• 反厄米特矩阵

反厄米特矩阵（Anti-Hermitian Matrix），也称为伴随矩阵（Adjoint Matrix），是指一个复数方阵，它满足以下两个条件：

1.矩阵的元素都是复数。

2.矩阵的共轭转置等于它自己的相反数的转置的复共轭，即 \(A = -A^H\) ，其中 \(A^H\) 表示矩阵 \(A\) 的共轭转置。

换句话说，反厄米特矩阵的每个元素关于主对角线反对称，并且每个元素与其对应位置的元素的共轭相等但符号相反。主对角线是从左上角到右下角的一条对角线。

正规矩阵一定可以对角化

特征值和特征向量

引用《线性代数的几何意义》的描述：“矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中，原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。”

大多数时候不用找到真正的一个几何例子，数学是这么一个东西。尝试用最简单的方式去理解一个思路，那么数学就会变得简单很多，以后解决问题也就更加直接有效。