学习一点数学基础，没学过的话也不可能真正理解 ai。 https://www.bilibili.com/video/BV1A24y1p76q/

线性空间的基于维数

线性空间中的线性变换

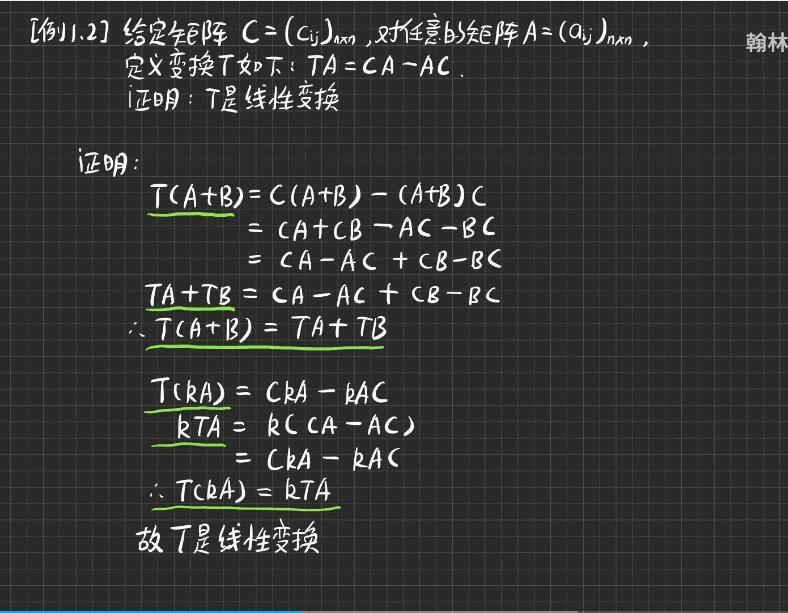
线性变换的像、核

这个稍微有一点抽像，但是花一点点的时间就理解了，也不是特别地抽象。

线性变换的矩阵

万物皆可矩阵化，线性变换 T 就是矩阵，就是这个间思。上图中的 C 过渡矩阵。矩阵和矩阵。学过且懂了。考试要求有步骤分。

定义是基底在前，变换在后。

求逆矩阵比较快的方法是用增广矩阵： \((A|E)\rightarrow(E | A^{-1})\) ，用初等变换法，A变成了单位矩阵之后，右面就变成了 \(A^{-1}\) 。

这里面的 \(\eta_{3}=(0, 1, 1)\) 图片显示不清楚。什么是单位矩阵？在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的 1，这种矩阵被称为单位矩阵。它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为 1。除此以外全都为 0。

性代基础。学数学要超纲学，才能在解基础题目时能做到降维打击。

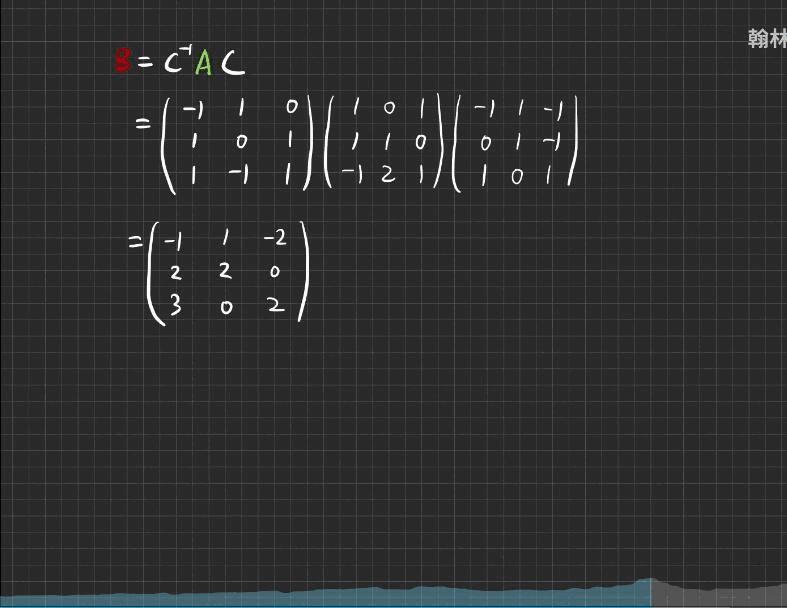
关键还是把过度矩阵写出来。