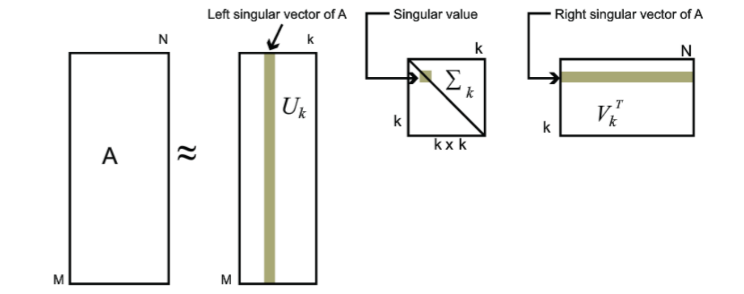
奇异值分解（SVD，Singular Value Decomposition）在人工智能（AI）和机器学习中的应用非常广泛，尤其是在数据降维、特征提取、推荐系统等方面。它的主要作用是将一个矩阵分解为三个矩阵的乘积，帮助我们从复杂的数据中提取重要的结构信息。以下是奇异值分解在人工智能中的几个关键应用：

1. 数据降维奇异值分解可以有效地用于数据降维，尤其是在处理高维数据时。通过SVD，我们可以将原始数据矩阵分解成三个矩阵，从而得到一个低秩的近似矩阵。这对于许多机器学习任务（如分类、回归、聚类等）非常有帮助，因为它能减少噪声、消除冗余，并提高计算效率。

   例如：

   在处理图像数据时，SVD可以用于将高维的图像数据降至较低维度，保留图像的主要信息，减少计算资源消耗。在文本分析中，SVD常用于潜在语义分析（LSA），它可以将词-文档矩阵降维，捕捉词汇之间潜在的语义关系，从而提高文本分类、情感分析等任务的效果。

2. 推荐系统在推荐系统中，奇异值分解被广泛用于从用户-物品交互矩阵中提取潜在的因子。传统的协同过滤方法通常依赖用户对物品的评分矩阵，而SVD可以通过将矩阵分解成多个低秩的因子，识别用户和物品之间的潜在关系，从而更好地预测用户可能喜欢的物品。

   例如：

   Netflix、Amazon等公司使用基于SVD的矩阵分解技术来构建推荐系统。通过分解用户与电影、商品的评分矩阵，SVD能够找到用户偏好的潜在模式，进而推荐他们可能感兴趣的电影或商品。

3. 特征提取与压缩在机器学习中，奇异值分解可以用来提取数据中的关键特征。这对于特征选择和数据压缩非常有用。通过SVD，我们可以找到那些对数据结构贡献最大的特征，并将其用于训练模型。

   例如：

   在文本处理中，SVD常用于特征提取，帮助机器学习模型从大量的文本数据中提取出最有意义的特征。在计算机视觉中，SVD用于图像压缩，通过保留最重要的奇异值和对应的奇异向量，减少图像数据的存储空间。

4. 噪声去除与信号恢复在许多实际应用中，数据往往包含噪声。奇异值分解能够通过保留较大的奇异值并忽略较小的奇异值，从而有效地去除噪声。对于信号处理或图像处理等任务，SVD有助于恢复原始信号并减少干扰。

   例如：

   在图像去噪中，SVD可以将图像矩阵分解，去除较小的奇异值，保留重要的结构信息，从而有效去除噪声。

5. 矩阵补全 SVD还可以用于矩阵补全任务，特别是在处理稀疏矩阵时。在推荐系统中，评分矩阵通常是非常稀疏的，SVD可以用来估算那些未被评分的位置，从而提供更准确的预测。

   例如：

   在电影推荐中，用户未评分的电影可以通过SVD补全，预测出用户可能的评分，从而给出个性化的推荐。总结奇异值分解在人工智能中的应用广泛且深入，主要体现在以下几个方面：数据降维，提高计算效率。推荐系统，通过矩阵分解揭示潜在的用户偏好。特征提取与压缩，帮助构建更简洁的模型。噪声去除与信号恢复，提高数据的质量。矩阵补全，解决稀疏数据问题。因此，SVD不仅是理论研究中的一个重要工具，也是实际工程中许多AI应用的核心技术之一。

这个是奇异值分解的原理，这是讲的最好的一篇博客：

https://www.cnblogs.com/pinard/p/6251584.html

奇异值分解有点类似于因式分解，压缩的方法有点类似于省略因子的多项式当中的小量。

奇异值分解的计算量比较大，感觉不应该考，这部分可以不花时间了吧。

奇异值分解的缺点：

SVD作为一个很基本的算法，在很多机器学习算法中都有它的身影，特别是在现在的大数据时代，由于SVD可以实现并行化，因此更是大展身手。SVD的原理不难，只要有基本的线性代数知识就可以理解，实现也很简单因此值得仔细的研究。当然，SVD的缺点是分解出的矩阵解释性往往不强，有点黑盒子的味道，不过这不影响它的使用。

关于转置与共轭转置的区别，我问了 GPT ： \(A^H\) 和 \(A^T\) 这两种写法在矩阵里是一样的吗？

SVD 对于实数矩阵用 \(A^T\) 就行了，但是对于复数矩阵，用 \(A^H\) ，问 GPT 为什么？

正交性是如何推广到酉性的？

至此我初步理解了酉性的由来，酉矩阵的由来，学会问 GPT 好的问题，可以方便的学习到关键的知识点。把所有的知识点全部学会，这样才能对问题有充分的认识。

关于复杂的专业书中的名词的含义，这绝对是高维多次的演变。比较“酉”这个字，中文最早见于商代甲骨文，其本义是酒器，引申指酒，又引申指成熟。后借以表示十二地支的第十位，又可以表示十二生肖中的“鸡”、蓄水的池塘等。但数学当中的“酉”性指的是 unitary 。这个英文的意思是统一的单一的含义。数学中暗指是一种自治的单一的特性，其实就是一组完整的坐标基。

举一个 svd 计算的例子，从 b 站当中找的视频（很怀念一群人一起学习的场景，这个世界，只为学习的学生时代是有限的，等真过了这个时代又会怀念，人生一直是喜欢远方，而觉得现在是苟且）：

https://www.bilibili.com/video/BV1YY4y1U7UX/?spm_id_from=333.337.search-card.all.click&vd_source=702481d9edf811d1f18266d09c074e00

上面部分要看奇异值有多少个，有多少个就取多少列，就是 \([v_1:v_2]\) 那块。这道题的解法和下面提到的解法并不是完全一样的。这道题上面的 \(\frac{2}{\sqrt{3}}\) 写错了。

再做一道题：

再看一道题：

https://www.bilibili.com/video/BV1ow411J7v8/?spm_id_from=333.788.recommend_more_video.0&vd_source=702481d9edf811d1f18266d09c074e00

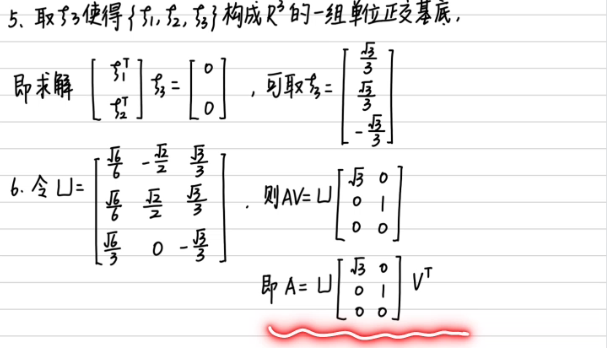
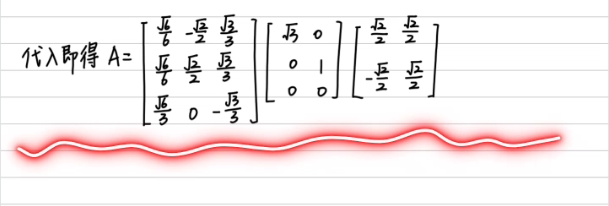
再做一道题：

记住任何一个矩阵A都可以分解成以下形式：

\(A=U\Sigma V^{T} \)

U V 均是酉矩阵，即满足 \(U^T U=I\) ， \(V^T V=I\)

U 是 \(A^T A\) 张成的矩阵，V 是 \(A^T A\) 张成的矩阵

\(\Sigma\) 是 \(AA^T\) 或者 \(A^T A\) 的特征值的平方根。

证明：

如何求解特征向量：

https://www.bilibili.com/video/BV1Js4y1372V/?spm_id_from=333.337.search-card.all.click&vd_source=702481d9edf811d1f18266d09c074e00

这么基础的东西！哎。自由未知量逐个设为 0 来写特征向量。

线代就是步骤较为繁琐。