机器学习流程:
特征工程建立模型评估与应用数据获取
特征工程的作用:
数据特征决定了模型的上限预处理和特征提取是最核心的算法与参数选择决定了如何逼近这个上限
特征如何提取:
segway 这个牌子的平衡车,有 handle(把手)和 wheel(轮子) handle,wheel -> Feature representation -> Leading Algorithm
传统的特征提取方法:
Natural images(自然界的图片)-> Learning bases: “Edges”
为什么需要深度学习:
32x32 的手写数字“3” -> 5x5 的 convolution(卷积核)处理,Feature Extraction -> fully connection(全连接)进行分类
深度学习的应用:
车辆检测人脸识别医疗(genomic data -> clinical data -> radiomic data)表情转换黑白图片转彩色图图片多分类 imagenet: https://www.image-net.org
深度学习算法优于传统人工智能算法
图像分类任务定义
绐图片加标签
计算机眼中的图像
是一个三维(三个通道)数组。数组的元素是色值(精度可以是 255)。数组的长度是像素数。像素数是 width * height 计算出。
CV 的挑战
照射角度形状改变部分遮蔽背景混入
CV 分类机器学习的常规套路
1.收集数据并给定标签 2.训练一个分类器 3.测试,评估
K 邻近(KNN)分类方法
1.计算已知类别数据集中的点与当前点的距离 2.按照距离依次排序 3.选取与当前点距离最小的 K 个点 4.确定前 K 个点所在类别的出现概率 5.返回前 K 个点出现频率最高的类别作为当前点预测分类
KNN 特点
KNN 算法本身简单有效,它是一种 lazy-learning 算法。分类器不需要使用训练集进行训练,训练时间复杂度为 0。 KNN 分类的计算复杂度和训练集中的文档数目成正比,也就是说,如果训练集中文档总数为 n,那么 KNN 的分类时间复杂度为 O(n)。 K 值的选择,距离度量和分类决策规则是该算法的三个基本要素。
图片数据库 CIFAR-10
经典数据集: 10 类标签 10000 个测试数据 50000 个训练数据
为什么 K 近邻不能用来图像分类?
背景主导是一个最大的问题,我们关注的却是主体(主要成分) 如何才能让机器学习到哪些是重要的成分呢?
KNN 中距离的概念: https://blog.csdn.net/kl1411/article/details/74079956
L1 (Manhattan) distance:
\( d_{1}(I_{1}, I_{2})=\sum\limits_{p} |I_{1}^{p}-I_{2}^{p}| \)
L2 (Euclidean) distance: \( d_{2}(I_{1}, I_{2})=\sqrt{\sum\limits_{p} |I_{1}^{p}-I_{2}^{p}|^{2}} \) 对于 k 邻近的 k 应该如何选择
背景主导是一个最大的问题,我们关注的却是主体(主要成分)。
通过网上这篇文章的讲解,我对 knn 的分类有了较为明了的认识:
https://blog.csdn.net/gengzhikui1992/article/details/104346235
通过交叉验证的方法来确定 k 值:
https://www.cnblogs.com/FYZHANG/p/12030460.html
通过 numpy 和 sklearn 来实现代码。
神经网络基础
- 线性函数
从输入到输出的映射。
在数学里对线性有详细的解释:https://www.zhihu.com/question/20084968
数学里,一般说的线性,是说的线性映射,这是一个函数(或称为映射,function or map),而不是方程(equation)。这个映射要同时满足两个条件:
1:可加性 \( f(x + y) = f(x) + f(y) \)
2:齐次性(同质性)\( f(\alpha x) = \alpha f(x) \)
也有用 叠加特性:\( f(ax+by)=af(x)+bf(y) \) 合起来表示的。
非线性方程,就是因变量与自变量之间的关系不是线性的关系,这类方程很多,例如平方关系、对数关系、指数关系、三角函数关系等等。求解此类方程往往很难得到精确解,经常需要求近似解问题。相应的求近似解的方法也逐渐得到大家的重视。
广义相对论方程就是一个非线性偏微分方程,无法得到精确解。广义相对论是描述引力的理论,它的方程式非常复杂。虽然这些方程式可以使用数值计算的方法求解,但是由于计算量很大,仍然是个非常困难的问题。不过,在某些特殊情况下,广义相对论的方程式可以被简化,从而得到一些精确解。例如,施瓦茨希尔德黑洞、克尔黑洞和台风模型等等,都是广义相对论的精确解。
人式智能中的线性函数为:
\( f(x_{i}, W, b) = Wx_{i}+b \)
stretch pixels into single column,理解一下。
损失函数
这个概念是核心:
目标函数(Objective Function),也称为损失函数(Loss Function)或代价函数(Cost Function),是在机器学习和优化问题中用来衡量模型预测结果与真实值之间差异的函数。
目标函数的选择取决于具体的任务和模型类型。在监督学习任务中,目标函数通常根据预测结果和真实标签之间的差异来评估模型的性能。对于回归问题,常用的目标函数包括均方误差(Mean Squared Error)和平均绝对误差(Mean Absolute Error)等;对于分类问题,常见的目标函数有交叉熵损失(Cross-Entropy Loss)和对数损失(Log Loss)等。
目标函数的设计旨在使模型的预测结果尽可能接近真实值,因此在训练过程中,优化算法会通过调整模型的参数,最小化目标函数的值。在机器学习的训练过程中,通常使用梯度下降等优化算法来求解目标函数的最小值。
需要注意的是,目标函数的选择应该与问题的特点和需求相匹配。不同的目标函数可能会导致不同的模型性能和训练效果。因此,在实际应用中,选择适当的目标函数对于模型的训练和性能优化非常重要。
损失函数,“预测更准确”即“loss”更小,损失函数的意义就在这里。
\( L_{i}=\sum_{j\neq{y_{i}}} max(0, s_{j}-S_{y_{i}}+1) \)
什么是损失函数?
一言以蔽之,损失函数(loss function)就是用来度量模型的预测值 f(x)与真实值 Y 的差异程度的运算函数,它是一个非负实值函数,通常使用 L(Y, f(x))来表示,损失函数越小,模型的鲁棒性就越好。
为什么要使用损失函数?
损失函数使用主要是在模型的训练阶段,每个批次的训练数据送入模型后,通过前向传播输出预测值,然后损失函数会计算出预测值和真实值之间的差异值,也就是损失值。得到损失值之后,模型通过反向传播去更新各个参数,来降低真实值与预测值之间的损失,使得模型生成的预测值往真实值方向靠拢,从而达到学习的目的。
有哪些损失函数?
还有就是百度的飞桨平台:
https://paddlepedia.readthedocs.io/
像 linux 内核一样的文档,总量也不多。可以从中学习到一些基础知识。自学的路从来打开,在互联网时代,一切知识都能自学。
- L2 范数均方差损失函数(MSE: Mean Square Error),Mean 是平均的意思:
\( L(Y|f(x))=\frac{1}{n}\sum_{i=1}^{N}{(Y_{i}-f(x_{i}))^{2}} \)
- L1 损失函数(即曼哈顿距离),又叫 MAE(Mean Absolute Error):
\(L(Y|f(x))=\sum_{i=1}^{N}{|Y_{i}-f(x_{i})|}\)
- 均方根误差损失函数(即欧式距离),又叫 RMSE(Root Mean Square Error):
\(L(Y|f(x))=\sqrt{\frac{1}{n}\sum_{i=1}^{N}{(Y_{i}-f(x_{i}))^{2}}}\)
- smooth L1 损失函数:
\[ \notag L(Y|f(x)) = \begin{cases} \frac{1}{2}(Y-f(x))^{2} & \text{ |Y-f(x)|<1} \\ |Y-f(x)|-\frac{1}{2} & \text{ |Y-f(x)|>=1} \end{cases} \]
Smooth L1 损失是由 Girshick R 在 Fast R-CNN 中提出的,主要用在目标检测中防止梯度爆炸。不懂的可以先不了解。后续再折回来看一下这个问题。
- huber 损失函数
\[ \notag {\displaystyle L_{\delta }(y,f(x))= {\begin{cases}{\frac {1}{2}}(y-f(x))^{2}&{\text{for }}|y-f(x)|\leq \delta , \\delta \ \cdot \left(|y-f(x)|-{\frac {1}{2}}\delta \right),&{\text{otherwise.}}\end{cases}}} \]
huber 损失是平方损失和绝对损失的综合,它克服了平方损失和绝对损失的缺点,不仅使损失函数具有连续的导数,而且利用 MSE 梯度随误差减小的特性,可取得更精确的最小值。尽管 huber 损失对异常点具有更好的鲁棒性,但是,它不仅引入了额外的参数,而且选择合适的参数比较困难,这也增加了训练和调试的工作量。
- KL 散度(相对熵)损失函数:
\(L(Y|f(x))=\sum_{i=1}^{n}{Y_{i}\times log(\frac{Y_{i}}{f(x_{i})})}\)
Y 代表真实值,f(x) 代表预测值。
相对熵由 Solomon Kullback 和 Richard Leibler 在 Kullback & Leibler (1951)中引入,属于数理统计当中的知识。
一种统计学度量,表示的是一个概率分布相对于另一个概率分布的差异程度,在信息论中又称为相对熵(Relative entropy)。
库尔贝勒莱布勒散度。外国人这么喜欢用人名命名公式吗?
- 交叉熵损失函数:
\(L(Y|f(x))=-\sum_{i=1}^{N}{Y_{i}log f(x_{i})}\)
交叉熵是信息论中的一个概念,最初用于估算平均编码长度,引入机器学习后,用于评估当前训练得到的概率分布与真实分布的差异情况。为了使神经网络的每一层输出从线性组合转为非线性逼近,以提高模型的预测精度,在以交叉熵为损失函数的神经网络模型中一般选用 tanh、sigmoid、softmax 或 ReLU 作为激活函数。
损失函数 = 数据损失 + 正则化惩罚项
\(L = \frac{1}{N}\sum_{i=1}^{N}\sum_{j\neq y_{i}}\max (0, f(x_{i};W)_{j} - f(x_{i};W)_{y_{i}}+1) + \lambda R(W)\)
正则化惩罚项:
\(R(W) = \sum_k\sum_l W_{k,l}^2\)
过拟合的模型是没有用的。通过对数据进行训练,得到模型参数。机器学习再认知上提供了一种思路,就是执果猜因。
L1 范数
什么是惩罚项呢?L1-norm,L2-norm 等,中文称 L1 正则化,L2 正则化,或者 L1 范数或 L2 范数。
下面这篇文章把正则化惩罚项讲的比较清楚了。
https://www.cnblogs.com/LXP-Never/p/10918704.html
L1 范数符合拉普拉斯分布,是不完全可微的。表现在图像上会有很多角出现。这些角和目标函数的接触机会远大于其他部分。就会造成最优值出现在坐标轴上,因此就会导致某一维的权重为 0,产生稀疏权重矩阵,进而防止过拟合。
最小平方损失函数的 L1 正则化:
\(W^{*} =\mathop{\arg\min\limits_{w}} \ \ \sum\limits_{j}\Big(t(x_{j})-\sum\limits_{i}w_{i}h_{i}(x_{j})\Big)^{2} + \lambda\sum\limits_{i=1}^{k}|w_{i}|\)
L2 范数
L2 范数符合高斯分布,是完全可微的。和 L1 相比,图像上的棱角被圆滑了很多。一般最优值不会在坐标轴上出现。在最小化正则项时,可以是参数不断趋向于 0,最后活的很小的参数。
在机器学习中,正规化是防止过拟合的一种重要技巧。从数学上讲,它会增加一个正则项,防止系数拟合得过好以至于过拟合。L1 与 L2 的区别只在于,L2 是权重的平方和,而 L1 就是权重的和。
如下,最小平方损失函数的 L2 正则化:
\(W^{*} =\mathop{\arg\min\limits_{w}} \ \ \sum\limits_{j}\Big(t(x_{j})-\sum\limits_{i}w_{i}h_{i}(x_{j})\Big)^{2} + \lambda\sum\limits_{i=1}^{k}w_{i}^{2}\)
如何选择损失函数?
(1) 选择最能表达数据的主要特征来构建基于距离或基于概率分布度量的特征空间。
(2)选择合理的特征归一化方法,使特征向量转换后仍能保持原来数据的核心内容。
(3)选取合理的损失函数,在实验的基础上,依据损失不断调整模型的参数,使其尽可能实现类别区分。
(4)合理组合不同的损失函数,发挥每个损失函数的优点,使它们能更好地度量样本间的相似性。
(5)将数据的主要特征嵌入损失函数,提升基于特定任务的模型预测精确度。
转载:https://zhuanlan.zhihu.com/p/261059231 ,另外 python 对这几种损失函数的实现也在这篇知乎的博客当中。
L1 范数和 L2 范数的区别:
1、L1 正则化是模型各个参数的绝对值之和。
L2 正则化是模型各个参数的平方和的开方值。
2、L1 会趋向于产生少量的特征,而其他的特征都是 0,产生稀疏权重矩阵。
L2 会选择更多的特征,这些特征都会接近于 0。
再讨论几个问题:
1.为什么参数越小代表模型越简单?
越是复杂的模型,越是尝试对所有样本进行拟合,包括异常点。这就会造成在较小的区间中产生较大的波动,这个较大的波动也会反映在这个区间的导数比较大。
只有越大的参数才可能产生较大的导数。因此参数越小,模型就越简单。
2.实现参数的稀疏有什么好处?
因为参数的稀疏,在一定程度上实现了特征的选择。一般而言,大部分特征对模型是没有贡献的。这些没有用的特征虽然可以减少训练集上的误差,但是对测试集的样本,反而会产生干扰。稀疏参数的引入,可以将那些无用的特征的权重置为 0.
3.L1 范数和 L2 范数为什么可以避免过拟合?
加入正则化项就是在原来目标函数的基础上加入了约束。当目标函数的等高线和 L1,L2 范数函数第一次相交时,得到最优解。
注意:
1、一般正则化,只是对模型的权重 W 参数进行惩罚,而偏置参数 b 是不进行惩罚的,而 torch.optim 的优化器 weight_decay 参数指定的权值衰减是对网络中的所有参数,包括权值 w 和偏置 b 同时进行惩罚。很多时候如果对 b 进行 L2 正则化将会导致严重的欠拟合,因此这个时候一般只需要对权值 w 进行正则即可。
2、torch.optim 的优化器固定实现 L2 正则化,不能实现 L1 正则化。
好了,现在对损失函数有了基本的了解了。
softmax 分类器
softmax 是一种激活函数。可以把得分值转换成一个 0 到 1 之间的概率值。形式是:
\(g(z)=\frac{1}{1+e^{-z}}\)
上面这个是 sigmod 函数。
有两种 loss function 比较重要:
Multiclass SVM loss 和 Softmax classifier loss
归一化的目的就是使得预处理的数据被限定在一定的范围内(比如[0,1]或者[-1,1]),从而消除奇异样本数据导致的不良影响。
softmax 又被称为归一化指数函数。
https://www.jiqizhixin.com/graph/technologies/0e9e62e2-9958-4146-b0af-f3d049ff2490
可以说 Softmax 函数是对 Sigmoid 函数的推广。
Sigmoid 函数(也称为逻辑函数或 Logistic 函数)是一种非线性函数,它将输入的实数映射到 0 到 1 之间的概率值。而 Softmax 函数是一种多元分类的激活函数,它将输入的实数向量映射为一组表示离散分类概率的向量。
在二元分类问题中,Sigmoid 函数常用于将线性组合的结果转化为一个类别的概率。而在多元分类问题中,Softmax 函数可以将线性组合的结果转化为多个类别的概率分布。Softmax 函数的数学形式如下:
\(softmax(Z_{i}) = \frac{e^{z^{i}}}{\sum_{j=1}^{k}e^{z_{j}}}\)
其中, \(z_{i}\) 表示线性组合的第 i 个元素的值(即 \(z = f(x_{i}; W)\) ),K 表示类别的数量。
因此,Softmax 函数可以被视为 Sigmoid 函数在多元分类问题中的推广。Softmax 函数保证了所有类别的输出概率之和为 1,因此可以用于多类别分类模型的输出层激活函数。
这个函数从形式的设计上来看并不复杂。用脑子简单想想也可以明白这个是怎么设计出来的。学习人工智能并不需要十分高深的数学知识。但是需要看懂公式,理解公式。
CE loss
softmax 的 loss 怎么算?
在多元分类任务中,交叉熵(Cross Entropy)常用于计算 Softmax 的 loss。交叉熵是一种用于衡量两个概率分布之间差异性的度量方法,通过比较模型预测的概率分布与真实标签的概率分布来度量模型的表现。
假设有 K 个类别, \(y_{i}\) 表示第 i 个样本的真实标签, \(\hat{y}_i\) 表示第 i 个样本对应的模型预测的概率分布,那么交叉熵的数学形式可以表示为:
\(CE(\hat y_{i}, y_{i})=-\sum\limits_{j=1}^{K}y_{i,j}\log(y_{i,j})\)
换个写法也可以写成: \(L_{i} = - \log P(Y=y_{i}|X=x_{i})\)
其中,\(y_{i,j}\) 表示第 i 个样本属于第 j 类的标签;\(\hat{y}_{i,j}\) 表示第 i 个样本属于第 j 类的预测概率。
而在训练过程中,我们需要将所有样本的交叉熵求和并除以样本数量 N,得到平均交叉熵损失,即:
\(J(\theta) = -\frac{1}{N}\sum_{i=1}^{N}\sum_{j=1}^{K} y_{i,j} \log(\hat{y}_{i,j})\)
其中,\(\theta\) 表示模型的参数。
Softmax 和交叉熵常常一起作为多元分类问题的 loss 函数,在反向传播时可以根据链式法则求出 Softmax 层和损失函数的梯度,并用于参数更新。
这些公式单列出来没有解释的话是看不懂的。
hinge loss(合页损失)
Hinge Loss(合页损失)是一种用于处理分类问题的损失函数,通常用于支持向量机(SVM)等算法中。
在二元分类问题中,假设我们需要将样本 xx 分为两个类别,1和-1。那么 Hinge Loss 的数学形式如下:
\(L(y, \hat{y}) = \max(0, 1 - y\cdot\hat{y})\)
其中,y 表示样本的真实标签,\(\hat{y}\) 表示样本的预测标签。
Hinge Loss 表明,在正确分类的情况下,该样本的损失为 0;而在错误分类的情况下,损失项被激活,并且与分类误差按线性递增的方式增加,即错误分类越严重,则损失项越大。该函数不仅度量了分类器的准确性,也可以用来鼓励有更大的间隔(Margin)的决策边界,从而提高了分类器对未知数据的泛化能力。
在多元分类问题中,可以使用 Multi-Class Hinge Loss(多分类合页损失)来计算损失,其数学形式如下:
\(L(y, \hat{y}) = \sum_{j \neq y} \max(0, \hat{y}_j - \hat{y}_y + \Delta)\)
其中,y 表示样本的真实标签,\(\hat{y}\) 表示样本的预测分数(Score),\(\Delta\) 是一个超参数,通常设置为 1。
Hinge Loss 在训练 SVM 等模型中被广泛使用,并被证明在分类问题上表现良好。
数据预处理归一化,损失函数正则化
https://blog.csdn.net/hrbeuwhw/article/details/79147275
正则化:就是平衡训练误差与模型复杂度的一种方式,通过加入正则项来避免过拟合(over-fitting)。
关于正则化,有一个 Elastic Net,吸收了 L1 和 L2 范式的优点。
归一化:1)归一化后加快了梯度下降求最优解的速度;2)归一化有可能提高精度。
什么是熵,什么是交叉熵
https://zhuanlan.zhihu.com/p/149186719
看完这篇文章,豁然开朗:
香农提出了熵的定义:无损编码事件信息的最小平均编码长度。
这个问题,我自己也想过,但是别人都提出理论了。理论的东西经过发展就会变得越来越成熟。
对于具有 N 种等可能性状态的信息,每种状态的可能性 P = 1/N,编码该信息所需的最小编码长度为(用二进制表示):
\(\log_{2}N = -\log_{2}\frac{1}{N}=-\log_{2}P\)
而熵的公式为:
\(Entropy = -\sum\limits_{i}P(i)\log_{2}P(i)\)
信息论中熵的概念和霍夫曼编码息息相关。
那什么是交叉熵呢?
“熵是服从某一特定概率分布事件的理论最小平均编码长度”,只要我们知道了任何事件的概率分布,我们就可以计算它的熵;那如果我们不知道事件的概率分布,又想计算熵,该怎么做呢?那我们来对熵做一个估计吧,熵的估计的过程自然而然的引出了交叉熵。
用公式来描述的话就是:
\(CrossEntropy=E_{x\sim P}[-\log Q(x)]\)
\(Entropy=E_{x\sim P}[-\log P(x)]\)
P 是真实的,经过观测得到的;而 Q 是理论的,也就是我们之前的模型。
score function
得分函数。
反向传播与梯度下降
梯度下降:
引入:当我们得到了一个目标函数后,如何进行求解?直接求解?(并不一定可解,线性回归可以当做是一个特例)
常规套路:机器学习的套路就是我交给机器一堆数据,然后告诉它什么样的学习方式是对的(目标函数),然后让它朝着这个方向去做
如何优化:一口吃不成个胖子,我们要静悄悄的一步步的完成迭代(每次优化一点点,累积起来就是个大成绩了)
梯度下降(Gradient Descent)是一种常用的优化算法,用于求解最小化目标函数的问题。它通过迭代方式更新模型参数,使得目标函数逐渐趋向于最小值。
在梯度下降算法中,我们首先需要定义一个目标函数(也称为损失函数),例如在机器学习中常用的均方误差(Mean Squared Error)。然后,我们从任意初始点开始,根据当前点的位置和梯度信息,以一定的步长(学习率)向梯度的反方向移动,不断迭代更新参数,直至达到局部或全局最小值。
具体来说,设目标函数为 \(J(\theta)\),其中 \(\theta\) 表示模型的参数,在梯度下降的过程中,我们按照以下步骤进行更新:
一、初始化参数:给定初始参数 \(\theta_0\)。二、计算梯度:计算当前参数位置的梯度,即 \(\Delta J(\theta)\)。三、参数更新:根据梯度和学习率 \(\alpha\),更新参数:
\(\theta_{t+1} = \theta_{t} - \alpha \nabla J(\theta_t)\)
四、其中,t 表示迭代的步数。重复步骤 2-3,直到满足停止条件,如达到最大迭代次数、梯度变化很小或损失函数收敛等。
梯度下降算法的关键在于计算目标函数的梯度,通过梯度信息来指导参数的更新方向。在实际应用中,有多种梯度下降算法的变体,如批量梯度下降(Batch Gradient Descent)、随机梯度下降(Stochastic Gradient Descent)和小批量梯度下降(Mini-batch Gradient Descent)等,以平衡计算效率和收敛速度。
梯度下降算法是机器学习和深度学习等领域中最基础且重要的优化方法之一,被广泛应用于模型训练和参数优化过程中。
- 什么是批量梯度下降?
批量梯度下降(Batch Gradient Descent)是梯度下降算法的一种形式,也是最原始的梯度下降方法之一。它在每一次迭代中使用全部训练样本的梯度计算来更新模型参数,因此也被称为全批量梯度下降。
具体来说,假设目标函数为 \(J(\theta)\),其中 \(\theta\) 表示模型的参数,批量梯度下降的更新公式为:
\(\theta_{t+1}=\theta_t-\alpha \frac{1}{m}\sum^m_{i=1}\nabla_{\theta} J(\theta_t,x^{(i)},y^{(i)})\)
其中,m 表示训练样本的数量,\((x^{(i)}, y^{(i)})\) 表示第 i 个样本的特征和标签,\(\alpha\) 表示学习率, \(\nabla_{\theta}\) 表示对参数 \(\theta\) 求偏导数的算符,\(\nabla_{\theta} J(\theta_t,x^{(i)},y^{(i)})\) 表示目标函数在参数 \(\theta_{t}\) 处关于第 i 个训练样本的梯度。这个式子的意义是,对所有的训练样本求平均值,然后用平均值作为梯度进行参数的更新。
批量梯度下降算法使用全部训练集的信息来更新参数,因此其估计结果比较准确,但是计算代价也比较高。此外,每次迭代需要遍历所有训练样本,所以在大样本数据集上训练,迭代速度会比较慢。
总之,批量梯度下降算法是一种基本的优化方法,被广泛应用于机器学习、深度学习等领域中。它的优缺点需要根据具体问题和数据规模来评估,可以通过其他变种的梯度下降算法来弥补其一些不足之处。
英文 nabla 是微分算符的意思。
- 什么是随机梯度下降
随机梯度下降(Stochastic Gradient Descent,SGD)是梯度下降算法的一种变体,它在每一次迭代中仅使用一个样本的梯度来更新模型参数。相比于批量梯度下降算法,SGD 的计算代价更低,能够加速模型的训练过程。
具体来说,在每次迭代中,SGD 从训练集中随机选择一个样本 \((x^{(i)}, y^{(i)})\),其中 \(x^{(i)}\) 表示该样本的特征, \(y^{(i)}\) 表示其对应的标签。然后,SGD 使用该样本的梯度来更新模型参数:
\(\theta_{t+1} = \theta_t - \alpha \nabla_{\theta} J(\theta_t, x^{(i)}, y^{(i)})\)
其中,\(\theta_t\) 表示第 t 个迭代时的参数值,\(\alpha\) 是学习率,\(\nabla_{\theta} J(\theta_t, x^{(i)},y^{(i)})\) 表示目标函数关于样本 \((x^{(i)}, y^{(i)})\) 在参数 $θ_t$处的梯度。
由于随机梯度下降每次只使用一个样本进行参数更新,因此其计算速度比批量梯度下降快。此外,SGD 还具有一定的随机性,这使得它在处理大数据集时能够避免陷入局部最优解,并且对于在线学习(Online Learning)等实时场景也具有较好的适应性。
然而,由于随机梯度下降仅使用一个样本的梯度来更新参数,因此在单个样本上的梯度估计可能存在较大的抖动。为了减小抖动并使训练过程更加稳定,通常会引入一些技巧,例如使用学习率衰减(Learning Rate Decay)、加入动量(Momentum)等。
总结来说,随机梯度下降是一种高效且常用的优化算法,在大规模数据集和实时学习中有着广泛的应用。
- 什么是小批量梯度下降法
小批量梯度下降(Mini-Batch Gradient Descent)是梯度下降算法的一种变体,它在每一次迭代中使用部分样本的梯度来更新模型参数。相比于批量梯度下降和随机梯度下降,小批量梯度下降综合了两者的优点,既可以减小计算代价,又能够在一定程度上保持梯度估计的稳定性。
具体来说,在每次迭代中,小批量梯度下降从训练集中随机选择一个固定大小的样本批次(mini-batch),假设该批次包含 m 个样本 \((x^{(i)}, y^{(i)})\),其中 \(x^{(i)}\) 表示第 i 个样本的特征,\(y^{(i)}\) 表示其对应的标签。然后,小批量梯度下降使用该批次的梯度的平均值来更新模型参数:
\(\theta_{t+1} = \theta_t - \alpha \frac{1}{m}\sum_{i=1}^{m} \nabla_{\theta} J(\theta_t, x^{(i)}, y^{(i)})\)
其中,\(\theta_t\) 表示第 t 个迭代时的参数值,\(\alpha\) 是学习率, \(\nabla_{\theta} J(\theta_t, x^{(i)},y^{(i)})\) 表示目标函数关于样本 \((x^{(i)}, y^{(i)})\) 在参数 \(\theta_t\) 处的梯度。
小批量梯度下降相比于批量梯度下降,其计算代价会小很多,因为每次迭代只需要处理一个批次的样本。同时,与随机梯度下降相比,小批量梯度下降能够减小梯度估计的抖动,提供更稳定的参数更新。此外,小批量梯度下降还可以充分利用并行计算的优势,提高训练过程的效率。
选择合适的小批量大小是一个重要的超参数,通常需要根据具体问题和计算资源进行调整。较小的批量大小可以提供更稳定的梯度估计,但会增加训练过程的噪声;较大的批量大小可以减小噪声影响,但可能会陷入局部最优解。
总之,小批量梯度下降是一种在实践中广泛应用的梯度下降算法,它在计算代价和稳定性之间取得了一个平衡,并能够有效地训练大规模数据集上的模型。
- 总结:
在深度学习和机器学习领域中,应用最广泛的梯度下降算法是小批量梯度下降(Mini-Batch Gradient Descent)算法。小批量梯度下降综合了批量梯度下降和随机梯度下降的优点,被广泛应用于训练神经网络等大规模数据集上的模型。
相较于批量梯度下降,小批量梯度下降具有更低的计算复杂度,因为每次迭代只处理一小部分样本,这使得它能够更高效地进行参数更新。与此同时,相比于随机梯度下降,小批量梯度下降在参数更新过程中能够提供更稳定的梯度估计,减少了抖动现象,并且能够充分利用并行计算的优势。
小批量梯度下降可以通过调整小批量的大小来平衡计算效率和模型稳定性,在实践中被广泛采用。通常情况下,小批量大小在几十到几千之间,具体的选择需要根据问题的复杂度、数据集的大小以及计算资源的限制进行权衡。
尽管小批量梯度下降是最广泛应用的梯度下降算法,但在特定的场景下也会使用其他变种的梯度下降算法。例如,当处理较小规模的数据集时,可以使用批量梯度下降;而在在线学习或者实时训练的场景下,随机梯度下降可能更适用。
总之,小批量梯度下降是目前应用最广泛的梯度下降算法,它提供了一种有效而稳定的方式来训练深度学习模型和其他机器学习模型。
学习率(步长):对结果会产生巨大的影响,一般小一些。
如何选择:从小的开始选,不行再小。
批处理数量:32,64,128 都可以,很多时候还得考虑内存和效率。
反向传播
neurons,神经元。关于反向传播这个概念,早就是一个基础概念了,但是在数学上,理解起来还是比较抽象,要反复看和理解。
算数和数学是不一样的东西。
矩阵求导:
https://zhuanlan.zhihu.com/p/32368246
https://zhuanlan.zhihu.com/p/24709748
https://zhuanlan.zhihu.com/p/24863977
反复看那些理解不了的公式,记住,公式中包含的信息是比较多的。如果不熟悉的领域要慢慢看才能看懂。不能急于求成。
行列式就是数值。矩阵是表示一种数据结构。
数学提问对于理解矩阵微分十分地重要,所以,下面这几个问题是我的一些疑惑。
- 矩阵于行列式不同吗?
矩阵和行列式是线性代数中的两个重要概念,它们有些相似但也有一定的区别。
矩阵(Matrix)是一个按照矩形排列的数表,其中的元素可以是实数或复数。矩阵通常用大写字母表示,例如 A、B 等。矩阵可以有不同的大小,通过行数和列数来描述。一个 \(m \times n\) 的矩阵具有 m 行和 n 列。每个矩阵元素可以通过索引标识,例如第 i 行、第 j 列的元素记作 \(A_{ij}\) 。
行列式(Determinant)是一个与方阵相关的标量值。方阵是一个行数和列数相等的矩阵。行列式的计算依赖于方阵的元素,通过展开定理或其他方法可以得到行列式的值。行列式的计算结果为一个数值,它包含了方阵多个元素之间的关系信息。行列式通常用竖线符号表示,例如 \(|A|\) 。
换句话说,矩阵是一种数据结构,用于存储和操作多个数值。而行列式是一个通过对方阵元素进行特定运算而得到的数值。
总结起来,矩阵是用来表示数据的结构,而行列式是通过矩阵的元素计算而来的特定数值。
列向量一般用“;”来分割元素。注意约定的写法。
- 行向量与列向量的区别?
行向量和列向量是矩阵中的两种特殊向量形式,它们在表示方式和运算规则上存在一些区别。
行向量:行向量是一个只有一行的矩阵,由左到右水平排列。行向量通常用小写字母加横线表示。行向量的转置得到的是列向量。
列向量:列向量是一个只有一列的矩阵,由上到下垂直排列。列向量通常用小写字母加箭头表示。列向量的转置得到的是行向量。
区别:
形状:行向量只有一行,而列向量只有一列。表示方式:行向量水平排列,列向量垂直排列。运算规则:行向量和列向量在进行矩阵乘法时需要遵循不同的规则。行向量与行数相同的矩阵相乘,结果为行向量;列向量与列数相同的矩阵相乘,结果为列向量。线性代数中的运用:行向量常用于表示方程组的系数矩阵,而列向量常用于表示方程组的解向量。需要注意的是,在计算机编程中,行向量和列向量有时也可以通过矩阵的转置来互相表示。但在数学中,行向量和列向量是不同的概念,它们在矩阵运算和表示方式上具有明确的区别。
- 多元微分学中的梯度怎么理解?
在多元微分学中,梯度是一个常用的概念,用于描述多变量函数在某一点的变化率和方向。
考虑一个具有多个自变量的函数,例如 f(x, y),其中 x 和 y 是自变量。梯度是这个函数对自变量的偏导数组成的向量。在二维情况下,梯度可以表示为 \(\nabla f = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)\) ,它是一个二维向量。在三维及以上的情况下,梯度是一个更高维度的向量。
梯度的几何意义可以理解为函数在某一点处最陡峭的上升方向。它指示了函数在该点最快增长的方向和速率。梯度的方向是函数在该点取得最大变化率的方向,而梯度的模(长度)表示了变化率的大小。
梯度在最优化问题中非常重要。在求解函数的最大值或最小值时,可以通过梯度信息来确定前进的方向。例如,在最小化函数时,可以朝着负梯度的方向进行迭代,从而逐渐接近最小值点。
总之,梯度在多元微分学中提供了关于函数在某一点的变化率和方向的信息。它在最优化、机器学习等领域中有着广泛的应用。
- 标量对向量的导数怎么理解?
标量对向量的导数,也称为向量的梯度,是一种向量函数,它描述了在某个点上一个标量函数对于相应向量变量在每个方向上的变化率和方向。
假设有一个标量函数 \(f(x_1,\ldots,x_n)\),其中 \(x_1,\ldots,x_n\) 是自变量,且同时存在一个向量 \(\mathbf{x}=(x_1,\ldots,x_n)\)。那么,标量 f 对向量 x 的导数就是一个向量,通常记作 \(\nabla f\),由函数 f 对每个自变量 \(x_i\) 的偏导数组成。即,
\(\nabla f = \left(\frac{\partial f}{\partial x_1}, \ldots, \frac{\partial f}{\partial x_n}\right)\)
梯度向量的符号表示通常为 \(\nabla\),由于它是一个向量,所以可以用一个箭头来表示。梯度向量的方向是变化最快的方向(即函数增加最快的方向),而梯度的大小表示函数在该点上的增长速率的大小。
例如,假设 \(f(x,y)=2x+y\) ,则 f 对于自变量向量 \(\mathbf{x}=(x,y)\) 的导数就是 \(\nabla f=\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)=(2,1)\) 。这意味着,在点(x,y)处,f 在 x 方向上每增加 1 个单位,f 将增加 2 个单位;而在 y 方向上每增加 1 个单位,f 将增加 1 个单位。
梯度向量在很多科学和工程领域中都有广泛的应用,包括优化、机器学习、物理学、工程学等。例如,在机器学习中,梯度被用来更新模型参数以最小化损失函数,从而提高模型性能。
- 什么是标量函数?
标量函数是一种以输入为向量或标量,输出为标量的函数。简单来说,它将一个或多个变量映射到一个实数,而不是向量或矩阵。
具体来说,考虑一个函数 f,它的定义域可以是一个或多个实数变量,例如 f(x)或 \(f(x_1,x_2,\ldots,x_n)\) 。如果该函数的值域为实数,那么它就是一个标量函数。
标量函数是最常见的函数类型,我们在日常生活中遇到的许多函数都属于这个类别。例如,温度、速度、能量、质量等都是标量的物理量,它们可以由标量函数来描述。
在数学和工程领域,我们经常需要研究和分析标量函数的性质,包括函数的连续性、可导性、最大值和最小值等。这些性质对于优化问题、最小二乘法、函数逼近等具有重要意义。通过对标量函数的研究,我们可以了解函数的行为、性质和变化规律,从而在实际问题中做出合理的决策和推断。
这里我看到 pdf 的 = 44 = 页了,做一个记录。
整体架构
模拟神经元。
神经网络的强大之处在于,用更多的参数来拟合复杂的数据。可以用非线性方程做堆叠,类似下面这样:
\(f=W_{3}\max(0, W_{2}\max(0, W_{1}x))\)
正则化的作用
惩罚力度对结果的影响:惩罚力度越大,拟合度越大,甚至过拟合。
参数个数对结果的影响:隐藏的神经元个数越多,拟合度越大,甚至过拟合。
激活函数
非常重要的一部分,常用的激活函数有:Sigmod , Relu , Tanh 等。
前两个函数的图像是从右向左,从高到低的两个滑梯,一个到 0 就滑到底了,另一个 0 的时候才滑到中间。一个光滑一个在 0 处有奇异点。
数据预处理
一、数据可以中心化: X -= np.mean(X, axis = 0) ,通过变换坐标系做到以原点为中心。
二、正则化:我的理解是把数据规范到一个范围内,比如 X /= np.std(X, axis = 0) 。
参数的初始化
通常我们使用随机策略来时空行参数初始化。肯定现在大模型用的都是预训练模型了。
参数的随机化举一个例子: W = 0.01* np.random.randn(D, H)
drop out
https://zhuanlan.zhihu.com/p/38200980
通过忽略一半的特征检测器(让一半的隐层节点值为 0),可以明显地减少过拟合现象。这种方式可以减少特征检测器(隐层节点)间的相互作用,检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。
语言模型 NLP
必读论文,emacs 读论文是最好用的。 https://browse.arxiv.org/pdf/1411.2738.pdf
读论文的技巧可以: https://www.cnblogs.com/xing901022/p/10161727.html
重中之重,CNN
ILSVRC : ILSVRC(ImageNet Large Scale Visual Recognition Challenge)是近年来机器视觉领域最受追捧也是最具权威的学术竞赛之一,代表了图像领域的最高水平。
在 2014 年到 2015 年,机器识别图片的准确性首次超过了人类。现在是 2023 年了,过去了 8 年了。2015 年的时候我刚毕业。没想到人老了,科技发展好似坐上了火箭。
检测、分类与检索、超分辨率重构,医学任务,无人驾驶,人脸识别都用到了 CNN 。
整体架构
分为输入层、卷积层、池化层、全连接层
卷积做了一件什么事
从 low-level feature 到 mid-level feature 到 high-level feature 再到 trainable classifier (可训练分类器)。
堆叠的卷积层。
卷积层涉及的参数:滑动窗口步长,卷积核尺寸,边缘填充,卷积核个数
卷积结果的计算公式:
长度: \(H_{2}=\frac{H_{1}-F_{H}+2P}{S}+1\)
宽度: \(W_{2}=\frac{W_{1}-F_{W}+2P}{S}+1\)
举例:输入数据是 32*32*3 的图像,用 10 个 5*5*3 的 filter 来进行卷积操作,指定步长为 1 ,边界填充为 2 ,最终输入的规模为?
(32-5+2*2)/1 + 1 = 32 ,所以输出规模为 32*32*10 ,经过卷积操作后也可以保持特征图长度、宽度不变。
卷积参数个数的计算:
还是上面的例子,用 10 个 5*5*3 的 filter 来进行卷积操作,总共需要多少个参数?需要: 5*5*3*10 + 10 = 760 个参数。
池化层
池化的意思就是压缩,也就是下采样。做的事情是什么样的呢?类似于把一张图片缩小的操作。常见的一种操作是最大池化。就是用 \(n \times n\) 的 filter ,用英文是 max pool with 2x2 filters and stride 2 。
一个典型的结构是下面这个样子的:
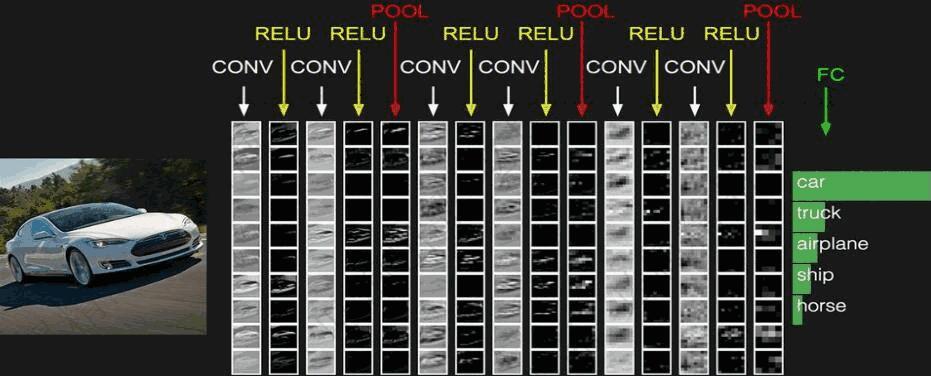
Figure 1: CNN 举例
特征图变化是: 卷积 -> 卷积 -> 池化 -> 卷积 -> 池化 -> 转换 -> 全连接
经典的 CNN 网络—— Alexnet
这个网络做了 13 层。
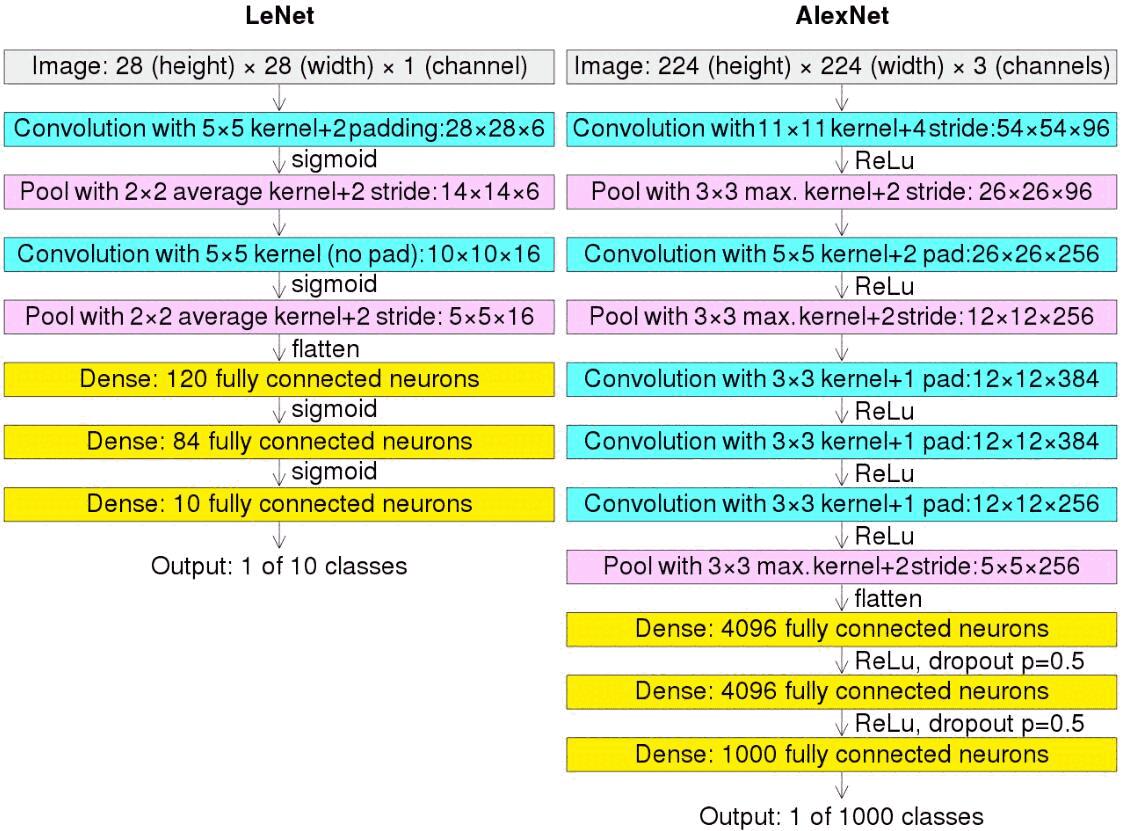
Figure 2: LeNet 和 AlexNet 网络
经典网络—— Vgg
敢想敢干,专注,坚持。如果没有走一条错误的路,那么最终的结果一定不会太差。事上无难事,只怕有心人,加油!
https://zhuanlan.zhihu.com/p/41423739
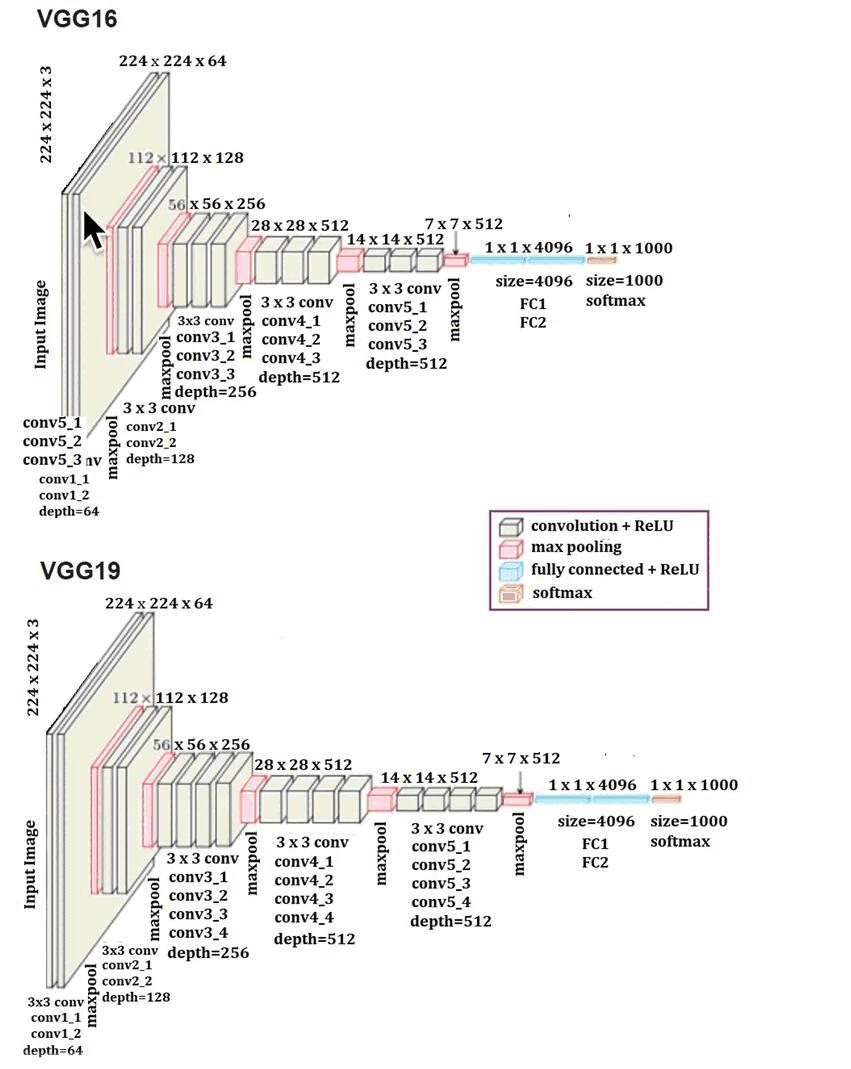
Figure 3: “caption”
VGG 增加了感受野的概念。最后的 7x7x512 拉平成 1x1x4096
VGG 优点
VGGNet 的结构非常简洁,整个网络都使用了同样大小的卷积核尺寸(3x3)和最大池化尺寸(2x2)。几个小滤波器(3x3)卷积层的组合比一个大滤波器(5x5 或 7x7)卷积层好:验证了通过不断加深网络结构可以提升性能。
VGG 缺点
VGG 耗费更多计算资源,并且使用了更多的参数(这里不是 3x3 卷积的锅),导致更多的内存占用(140M)。其中绝大多数的参数都是来自于第一个全连接层。VGG 可是有 3 个全连接层啊!
PS:有的文章称:发现这些全连接层即使被去除,对于性能也没有什么影响,这样就显著降低了参数数量。
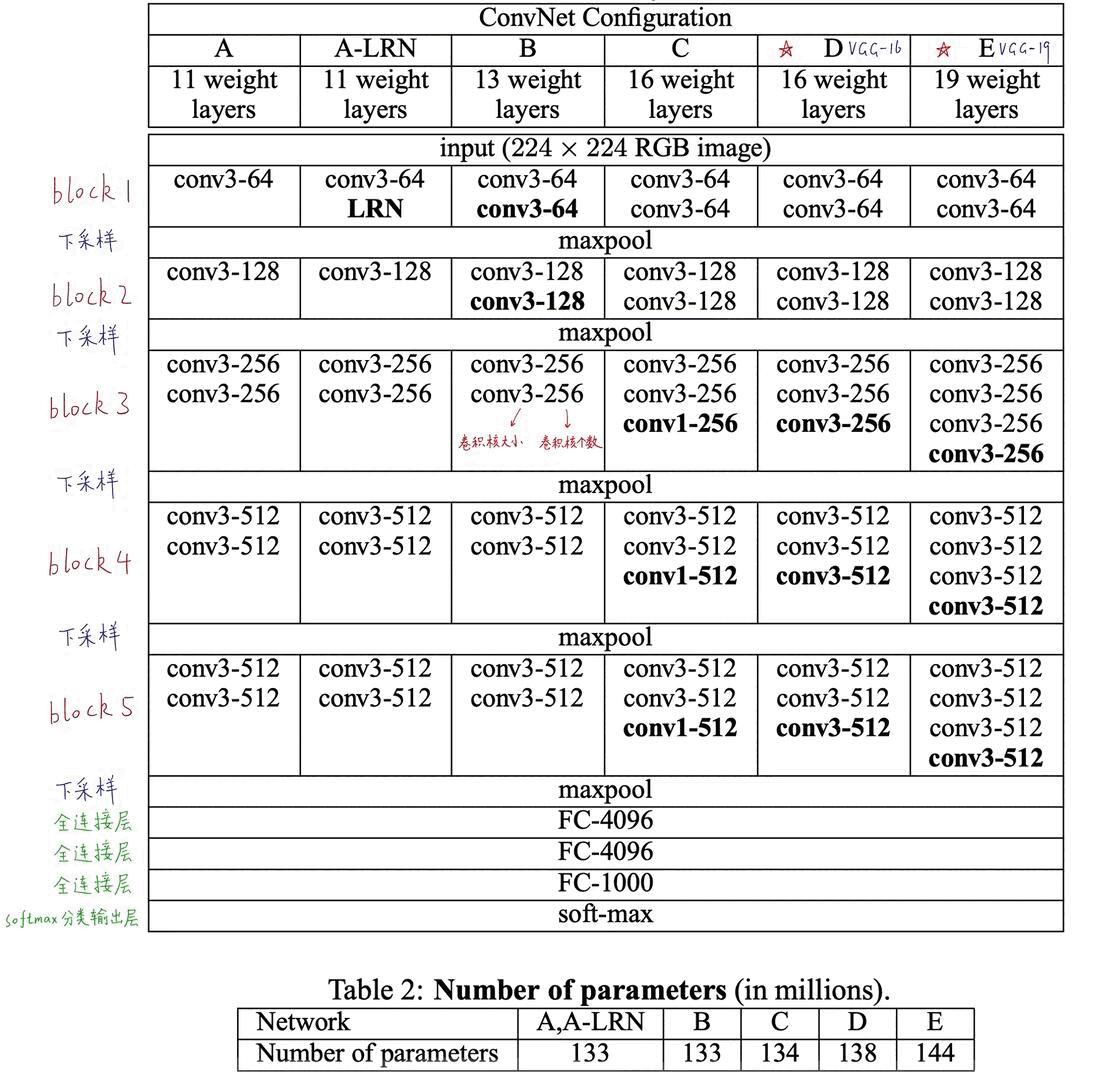
Figure 4: “caption”
还有最下面的一层是 soft-max 层,输出的是一千个类别的后验概率。是 0 到 1 之前的求和概率,并且这些概率求和为 1 。
卷积的作用是用于特征提取,训练出来的卷积就会按某种规则提取出来一种特征。但是结果是训练出来的。
信号处理中的卷积和数字图像处理中的卷积完全是不同的:https://blog.csdn.net/chaipp0607/article/details/72236892 计算的方法有相似之处。卷积的定义是:卷积是两个变量在某范围内相乘后求和的结果。缩小范围,产生影响的结果。这个就是 CNN 本质的东西。从数学上来说的本质是相同的,只不过一个空间中包含时域,另一个空间中只包含视野。
全连接层起到的是“分类器”的作用。但是作用不限于分类器,FC 的意义还是非常地复杂的: https://www.zhihu.com/question/41037974 ,但是粗略的讲,就是分类器。网上讲的东西非常地好,我其实不太用花钱学习。
我感觉学完了经典的 CNN 网络模型,ai 的知识不学完了一半了。当然,这是我瞎扯的,来源于一个初学者的抖激零。
更深的网络模型需要用残差等设计。学院派模型最深,就是到了 VGG 19 这种了。了解其原理之后。好的东西会保留。坏的东西会扬弃。最后感觉是殊途同归。ai 真的很有趣。值得一生学习和钻研。
https://www.bilibili.com/video/BV1fU4y1E7bY/ ,这里有精读 VGG 论文的课程。 = 我最感兴趣的地方是 AI 情绪化 =
这种东西可以让 AI 变得更加有趣,可以应用在游戏里,还能用在电影和有趣的视频制做上面。这个好的想法一旦能实现,以后肯定有很多人会喜欢。
同济子豪兄的视频非常的好,只有学到了一定的阶段才知道自己要学一些什么东西。https://space.bilibili.com/1900783
VGG-16 当年获得了识别的第二名,定位的第一名。
它是把像素空间的信息转化成语义空间的信息。
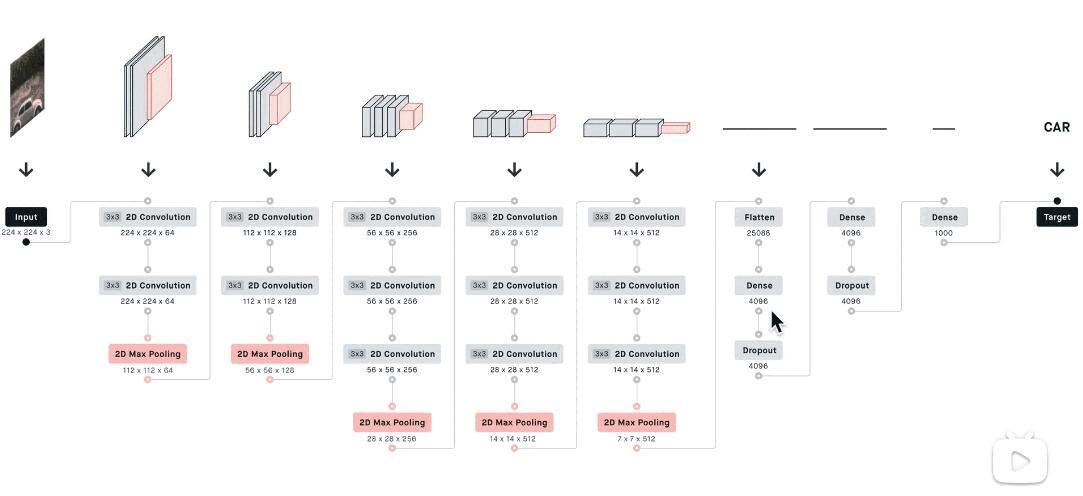
Figure 5: “caption”
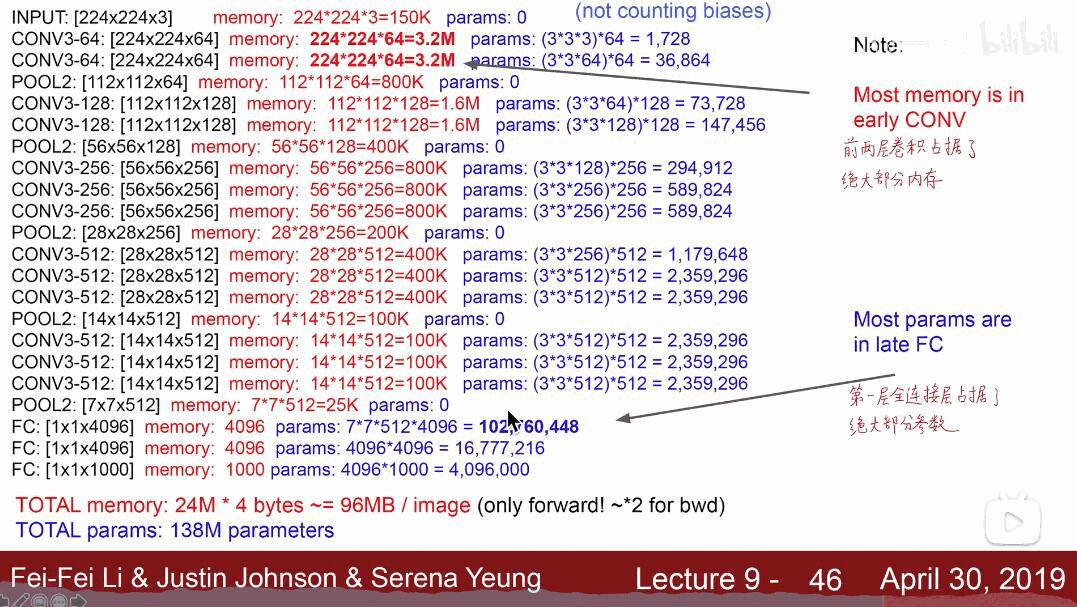
Figure 6: “caption”
这部分的空间只是算了前向传播的,反向传播的空间占用没有算,梯度参数需要占用内存。
两个 3x3 的卷积核可以代替一个 5x5 的卷积。想像一下,5x5 的一个图像被 3x3 的卷积核做一次运算,只剩下一个 1x1 的了。而同样的,用一个 5x5 的卷积核,只需要做一次,就可以变成 1x1 的。从这个角度来等价的。
优点,参数的个数由 25 个变成了 9 个。表示的线性。三层 3x3 代替一层 7x7 的卷积核。还有一个好处,它是最小的包含左,右,上,下等概念的一个单元。
在 inception 模型中也有这样的做法。还把 3x3 的卷积分解为了 1x3 的卷积和 3x1 的两个卷积。
后面出现的 inception-v3 ,v4 和 Resnet 都超过了它。下面是 2017 年的对比图。之前的都称之为古典时期的了。
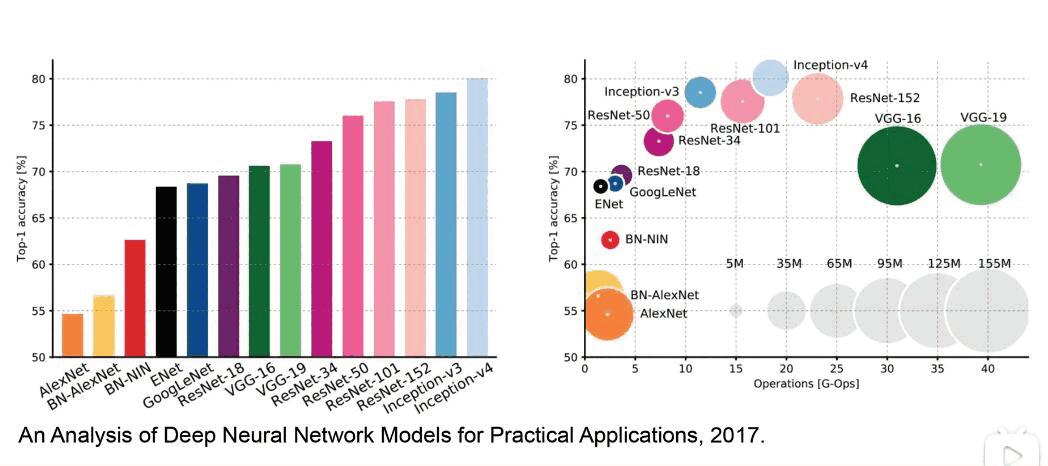
Figure 7: “caption”
圆圈大小是参数的数量。
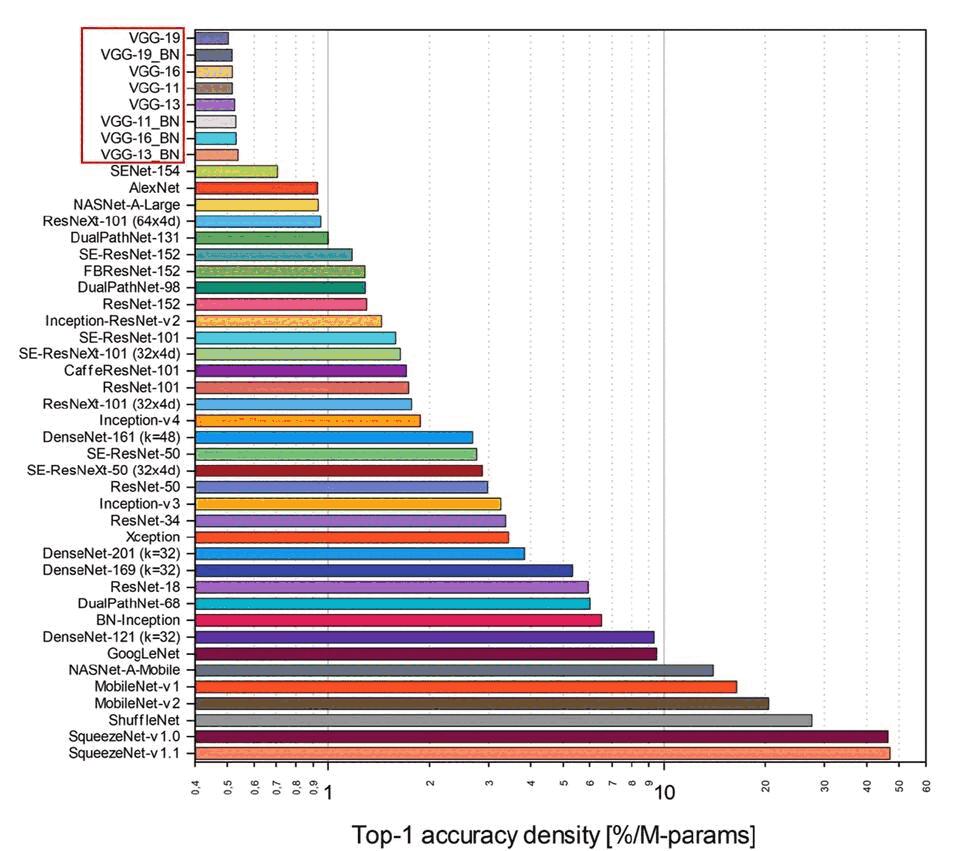
Figure 8: “caption”
vgg 的参数效率是非常差的。好的是下面的三个:SqueezeNet , ShuffleNet , MobileNet 这些轻量化网络。性能好,参数好。
vgg 原版的报告在: http:/www.robots.ox.ac.uk/~karen/pdf/ILSVRC_2014.pdf
人工智能是一门实验的科学。在辅以粗犷的理论加以解释。但是这种直觉有其科学性,可以说它是一门精确的玄学科学。需要极悟之道。
更多的论文精讲可以选择先不看。等到有兴趣的时候再仔细研究。它使用的 ReLU 激活函数。它会引入更多的非线性,这句话放在论文当中没有数学证明,岂不是玄学吗?
原论文的细节很多,涉及随机初始化,还有一堆其它的东西。东西有点小多,我想先不顾及其细节。
很明显,堆叠小的卷积核所需的参数更少一些,并且卷积过程越多,特征提取也会越细致,加入的非线性变换也随着增多,还不会增大权重参数个数,这就是 VGG 网络的基本出发点,用小的卷积核来完成体特征提取操作。
经典网络—— Resnet
不同损失函数的选择有什么道理?ResNet 的作者何恺明也因此摘得 CVPR2016 最佳论文奖。也就是我刚毕业那会儿,人工智能的早期发展正如火如荼的进行中。
我们知道深层网络存在着梯度消失或者爆炸的问题,这使得深度学习模型很难训练。但是现在已经存在一些技术手段如 BatchNorm 来缓解这个问题。因此,出现深度网络的退化问题是非常令人诧异的。
基本假设:现在你有一个浅层网络,你想通过向上堆积新层来建立深层网络,一个极端情况是这些增加的层什么也不学习,仅仅复制浅层网络的特征,即这样新层是恒等映射(Identity mapping)。在这种情况下,深层网络应该至少和浅层网络性能一样,也不应该出现退化现象。好吧,你不得不承认肯定是目前的训练方法有问题,才使得深层网络很难去找到一个好的参数。
ResNet 的一个重要设计原则是:当 feature map 大小降低一半时,feature map 的数量增加一倍,这保持了网络层的复杂度。
https://zhuanlan.zhihu.com/p/31852747
讲完了 Resnet 就剩下 DenseNet 等了。何凯明大佬厉害啊。
https://kaiminghe.github.io/ ,这是人类的数据科学家啊,智力与运气并存,牛人。这人是广东 04 年的状元。
什么是残差网络,这个从 b 站上找一些东西,直接搜就有很多。
知乎上讲残差网络: https://zhuanlan.zhihu.com/p/42706477 ,这个人收集的其它的一些文章也是非常地好的。数学公式很多,可能刚开始也不一定理解,但是后面还是要深入去啃一下的。
b 站上对上面知乎的讲解:https://www.bilibili.com/video/BV1rZ4y1m7d9/ ,此人是范仁义。多跟随一些大牛的脚步,人类的发展是随机的一种行为。
https://www.zhihu.com/collection/277253986
\(X_{l+1}=X_{l}+F(x_{1},W_{l})\) 这个核心公式的意思是,下一层是输入是上一层的输入加上一个东西。
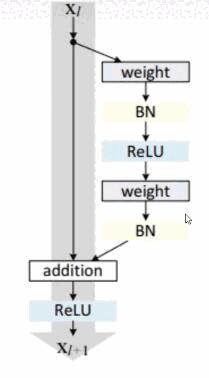
BN 就是批归一化。这样会让每一层的信息在传递过程中不会丢失掉太多。 feature map 。上面就是一个残差块的过程。可以叠加两个残差块。
为什么 1x1 的卷积可以减少计算量,又不损失太多的信息。用多个卷积核提取到多个特征,对应的特征比较少,少部分的可以提取到特征,大部分无法提取到特征。这个是一个稀梳的东西,就可以进行降维并且不损失太多的信息了。
b 站上搜 ResNet 代码实战,就有找到很多很好的视频啊。
经典网络—— DenseNet
人工智能网上的教程太多了,想学的话一定会有无数的方法可以把它们学好。我现在仅仅看到第二部分,就已经感觉收获了很多的知识,如果看完后面的几部分。再多学习几遍,一定可以搞清楚大部分浅显的内容。至于深刻的内容,可能要有了足够的经验,并且对数学有了更清楚的更解之后才行。
这些经典的网络模型可以用 python 来跑一跑。打开代码看一看。大模型的答案越是像人,无限的接近就是等于。虽然说看起来它并有思想,只是把人类的思想以某种形式固化了下来。随着时间的发展,这个世界绝对会越来越精彩的。
经典网络—— RNN 网络
与 CNN 不一样的是 RNN 主要用于 NLP 领域。RNN 主要用于处理序列数据,如文本、音频和时间序列数据,它们具有循环结构,可以考虑数据之间的时序关系。
CNN 可以用于文本分类。
LSTM ——长知时记忆网络
Hierarchical Softmax
GAN
支持向量机(svm)
支持向量机和深度学习有什么区别?
https://worktile.com/kb/p/62894 ,
现在工业上最先进的是 GBDT 了。GBDT(Gradient Boosting Decision Tree)是一种基于决策树的集成学习算法,也被称为梯度提升树。它通过逐步迭代地训练多个决策树模型,每次迭代都在之前模型的残差上训练新的模型,最终将所有模型的预测结果加权求和得到最终结果。由于 GBDT 具有很强的泛化能力和鲁棒性,因此在各种机器学习任务中广泛应用,如分类、回归等。
逻辑回归与 SVM 的损失函数不同,逻辑回归采用的是平方损失函数,SVM 采用的是合页损失函数。但是两种损失函数的目的是相同的,都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。SVM 的合页损失函数有一块“平坦”的零区域,使得支持向量的解具有稀疏性,而逻辑回归的损失函数是光滑的单调函数,没有支持向量的概念,逻辑回归更依赖于更多的数据,受数据分布的影响。逻辑回归的输出具有自然的概率意义,即给出预测标记的同时也给出了概率,而支持向量机不具有概率意义。SVM 依赖数据表达的距离测度,所以需要对数据先做 normalization;逻辑回归不受其影响。
什么是支持向量?
支持向量是支持向量机(SVM)算法中的概念。在 SVM 中,支持向量指的是训练数据中对决策边界(或者称为超平面)位置有影响的样本点。这些样本点恰好位于各自类别的边界上,它们决定了最终的决策边界的位置。在 SVM 算法中,只有这些支持向量才对最终的分类决策起作用,其他样本点则不会对决策边界产生影响。
支持向量机通过找到能够正确划分不同类别样本的决策边界,并且使得支持向量到决策边界的距离尽可能远,从而实现对数据的有效分类。这种方法使得支持向量机在处理高维数据和复杂数据特征时具有很好的性能表现。
svm 本质上还是“浅度学习”,不带核函数的 svm 只能线性分类。带核函数也本质上是把线性不可分问题映射到一个可分问题上,本质还是线性分类。然而这个映射函数的构造并不容易,多数问题即使映射到高维它还是线性不可分。svm 本质上只有一层,所以是“浅度学习”。
逻辑回归不是深度学习算法,它属于传统的机器学习算法。深度学习是一种基于神经网络的机器学习方法,它通过多层的神经网络结构来学习和提取数据的高阶特征表示。
逻辑回归是一种用于二分类问题的线性模型,它通过将输入特征与权重相乘并加上偏置项,然后将结果通过一个 sigmoid 函数进行映射,得到样本属于正类的概率。逻辑回归主要用于处理线性可分的二分类问题,并且可以通过最大似然估计等方法进行参数的优化。
相比之下,深度学习是一种更为复杂的模型,它可以通过多个隐藏层来学习和表示非线性的数据特征,具有更强大的表达能力和学习能力。深度学习在处理大规模数据和复杂任务时通常表现出色,但也需要更多的计算资源和训练时间。
杂谈
中国人喜欢说打好基本功,小学和初等教肓做的还是那么一回事。但是中国人是最浮躁的,企业的短视和降本增效,个人的追求功名利禄。大学教肓课本缺少由来的讲解,只讲如何做题和做运算。追求真理和本质是对的,可是中国人,外行领导内行。聪明人因为文化也大都急功近利。国人的人性既然有缺点,那这社会就应该吃下这份苦果。也不只是中国人,人本来就是有劣性的。人的高尚的一面只有在少数情况下才会显现出来,大多数情况下很难做好。这是正常的。
只是自己能做好一点吗?自己能比多数我说到的人做的好就行了。但行好事,莫问前程。管你想活与否,一个人也就这几十年,怎么过,自己能做出很多的决定,按照自己的目标过好每一天。
人工智能是以线性的计算模拟非线性的意识,因为非线性的问题不好求解,有求解的方法,但是人没有找到统一的方法。人类可以依靠对世界的感知,综合,创造新的工具,并借助新的东西,拓宽认知的边界。如果机器可以做到这一点,那就可以说它成为了一种强人工智能了。
一个可以找代码片段的网站
这个真心是很不错的,看一些代码,用 emacs 跑一跑,调试一下,理解一下。paddle 这个框架也是可以的,他好就是好在是国内的一个 AI 框架。这个 AI 框架起码下载和调试起来是比较方便的。框架大体是类似的,都是可用的,还有国内的文档,这么好的学习路径,赶紧能用起来才是最重要的。
学习路径
先安装 conda ,再安装 CPU 版本的 paddle 。
再 emacs 打开 python 项目。
尝试用 paddle 来写一些经典的网络模型,找一些开源的数据集做一些测试。
就这么办,哪怕是一些简单的代码,能做单元测试,能 run 起来,理解原理就足够了。好,也不好。
